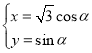题目内容
【题目】已知椭圆![]() ,
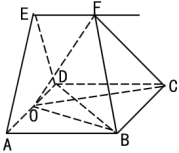
,![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 长轴的左、右端点,
长轴的左、右端点,![]() 为椭圆上的动点.
为椭圆上的动点.
(1)求![]() 的最大值,并证明你的结论;
的最大值,并证明你的结论;
(2)设直线![]() 的斜率为
的斜率为![]() ,且
,且![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
【答案】(1)![]() 的最大值为
的最大值为![]() ;证明见解析(2)
;证明见解析(2)![]()
【解析】
(1)设![]() ,(
,(![]() ,
,![]() ),过点
),过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,由三角函数的概念可得
,由三角函数的概念可得 ,
, ,由两角和的正切公式可得
,由两角和的正切公式可得![]()
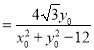 ,求出
,求出![]() 后由椭圆对称性即可得解;
后由椭圆对称性即可得解;
(2)由题意可知![]() ,利用
,利用![]() 即可得
即可得![]() ,由
,由![]() 的取值范围即可求得
的取值范围即可求得![]() 的取值范围,即可得解.
的取值范围,即可得解.
(1)根据椭圆的对称性,不妨设![]() ,(
,(![]() ,
,![]() ).
).
过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,则
,则![]()
![]() ,
,
于是,有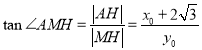 ,
,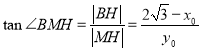 ,
,
![]()
![]()
![]()
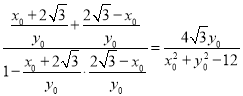 ,
,
![]() 点
点![]() 在椭圆
在椭圆![]() 上,
上,
![]()
![]() ,
,![]()
![]() ,
,![]()
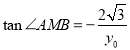 ,
,
而![]() ,
,
![]()
 ,
,
![]()
![]() ,
,
![]()
![]() 的最大值为
的最大值为![]() ,此时
,此时![]() ,即点
,即点![]() 为椭圆
为椭圆![]() 的上顶点.
的上顶点.
根据椭圆的对称性,当点![]() 为椭圆
为椭圆![]() 的短轴的顶点时,
的短轴的顶点时,![]() 取最大值,其最大值为
取最大值,其最大值为![]() .
.
(2)设直线![]() 的斜率为
的斜率为![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]()
![]() ,
,
又![]() ,
,![]()
![]() ,
,
![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,
故直线![]() 的斜率的取值范围为
的斜率的取值范围为![]() .
.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目