题目内容
观察:
(1×2-0×1)=1;
(2×3-1×2)=2;
(3×4-2×3)=3;
(4×5-3×4)=4.
由上述事实你能得出怎样的结论
[n(n+1)-(n-1)n]=n,n∈N*
[n(n+1)-(n-1)n]=n,n∈N*.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由上述事实你能得出怎样的结论
| 1 |
| 2 |
| 1 |
| 2 |
分析:由于:
(1×2-0×1)=1;
(2×3-1×2)=2;
(3×4-2×3)=3;
(4×5-3×4)=4,…左边分别是
[n(n+1)-(n-1)n],n=1,2,3,4,右边是n,n=1,2,3,4,由此即可确定第n个等式.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵
(1×2-0×1)=1;
(2×3-1×2)=2;
(3×4-2×3)=3;
(4×5-3×4)=4,…
∴第n个等式为
[n(n+1)-(n-1)n]=n,n∈N*,
故答案为:
[n(n+1)-(n-1)n]=n,n∈N*
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴第n个等式为
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:此题主要考查了数字的变换规律及归纳推理,解题的关键是正确把握题目隐含的规律解决问题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
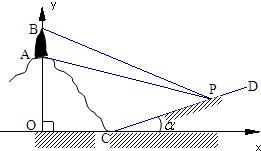 如图所示,某人在斜坡P处仰视正对面山顶上一座铁塔,塔高AB=80米,塔所在山高OA=220米,OC=200米,观测者所在斜坡CD近似看成直线,斜坡与水平面夹角为α,
如图所示,某人在斜坡P处仰视正对面山顶上一座铁塔,塔高AB=80米,塔所在山高OA=220米,OC=200米,观测者所在斜坡CD近似看成直线,斜坡与水平面夹角为α,