题目内容
已知各项为正数的等差数列{an}的前20项和为100,那么a7•a14的最大值为
- A.25
- B.50
- C.100
- D.不存在
A
分析:设出等差数列的通项公式和前n项和公式分别为an=a+(n-1)d,sn=na+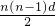 ,由前20项和为100得到2a+19d=10,而a7+a14=(a+6d)+(a+13d)=2a+19d=10,所以利用基本不等式a+b≥2
,由前20项和为100得到2a+19d=10,而a7+a14=(a+6d)+(a+13d)=2a+19d=10,所以利用基本不等式a+b≥2 当且仅当a=b时取等号,且a,b为正数,得到a7•a14的最大值即可.
当且仅当a=b时取等号,且a,b为正数,得到a7•a14的最大值即可.
解答:设等差数列首项为a,公差为d,则an=a+(n-1)d,sn=na+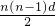 ,
,
因为前20项和为100得s20=20a+190d=100即2a+19d=10
所以a7+a14=(a+6d)+(a+13d)=2a+19d=10,
因为各项为正,所以a7+a14≥2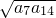 即a7•a14≤
即a7•a14≤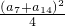 =25
=25
所以a7•a14的最大值为25
故选A
点评:考查学生运用等差数列性质的能力,以及利用基本不等式证明的能力,掌握等差数列的通项公式和求和公式的能力.
分析:设出等差数列的通项公式和前n项和公式分别为an=a+(n-1)d,sn=na+
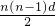 ,由前20项和为100得到2a+19d=10,而a7+a14=(a+6d)+(a+13d)=2a+19d=10,所以利用基本不等式a+b≥2
,由前20项和为100得到2a+19d=10,而a7+a14=(a+6d)+(a+13d)=2a+19d=10,所以利用基本不等式a+b≥2 当且仅当a=b时取等号,且a,b为正数,得到a7•a14的最大值即可.
当且仅当a=b时取等号,且a,b为正数,得到a7•a14的最大值即可.解答:设等差数列首项为a,公差为d,则an=a+(n-1)d,sn=na+
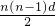 ,
,因为前20项和为100得s20=20a+190d=100即2a+19d=10
所以a7+a14=(a+6d)+(a+13d)=2a+19d=10,
因为各项为正,所以a7+a14≥2
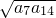 即a7•a14≤
即a7•a14≤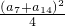 =25
=25所以a7•a14的最大值为25
故选A
点评:考查学生运用等差数列性质的能力,以及利用基本不等式证明的能力,掌握等差数列的通项公式和求和公式的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知{an}为各项均为正数的等比数列,Sn是它的前n项和,若a2•a3=2a1,且a4与a6的等差中项为
,则S4=( )
| 5 |
| 4 |
| A、35 | B、33 | C、30 | D、29 |
 满足
满足 (
( ),且
),且 是
是 的等差中项,则数列
的等差中项,则数列 满足
满足 ,且
,且 是
是 的等差中项.
的等差中项.  ;
; ,求使
,求使 成立的正整数n的最小值.
成立的正整数n的最小值.