题目内容
(12分)在三棱柱ABC-A1B1C1中,△ABC与△A1B1C1都为正三角形且AA1⊥面ABC,F、F1分别是AC,A1C1的中点。

求证:(1)平面AB1F1∥平面C1BF;
(2)平面AB1F1⊥平面ACC1A1.
(1)详见解析;(2)详见解析.
【解析】
试题分析:(1)要证 ,只需证
,只需证 、
、 ,只需证
,只需证 、
、 ,而四边形
,而四边形 、四边形
、四边形 皆为平行四边形,所以得证;(2)要证
皆为平行四边形,所以得证;(2)要证 ,只需证
,只需证 ,只需证
,只需证 、
、 ,其中易知
,其中易知 可得
可得 ,△A1B1C1 为正三角形可得
,△A1B1C1 为正三角形可得 ,从而得证.
,从而得证.
试题解析:(1)连接 ,在三棱柱
,在三棱柱 中,由
中,由 为棱的中点,所以
为棱的中点,所以 ,四边形
,四边形 是平行四边形,所以
是平行四边形,所以 ,又
,又 ,
, 则
则 .又在矩形
.又在矩形 中可得
中可得 ,且
,且 ,
, ,则
,则 ,而
,而 ,
, 且
且 ,所以
,所以 .
.
(2)因为 ,
, ,所以
,所以 ,又因为△A1B1C1 为正三角形,
,又因为△A1B1C1 为正三角形, 的中点,所以
的中点,所以 ,又
,又 ,所以
,所以 ,因为
,因为 ,所以
,所以 .
.
考点:(1)面面平行的判定;(2)面面垂直的判定.

练习册系列答案
相关题目
若圆x2+y2=4上每个点的横坐标不变.纵坐标缩短为原来的 ,则所得曲线的方程是( )
,则所得曲线的方程是( )
A. | B. | C. | D. |
 ,且经过点
,且经过点 的圆的标准方程为 .
的圆的标准方程为 .  ,其中
,其中 为向量
为向量 与
与 的夹角,若
的夹角,若 ,
, ,
, ,则
,则 等于( )
等于( ) ,则( )
,则( ) B.
B.
 D.
D.
 异面,
异面, 异面,则
异面,则 异面;
异面; ,则
,则 所成的角相等;
所成的角相等; ,
, ,则
,则 .
. 为定义在R上的奇函数,且在
为定义在R上的奇函数,且在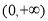 内是增函数,又
内是增函数,又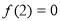 ,则不等式
,则不等式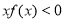 的解集为( )
的解集为( )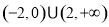

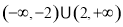
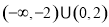
 在区间
在区间 上单调递增,且在这个区间上的最大值是
上单调递增,且在这个区间上的最大值是 ,那么
,那么
 B.
B. C.2 D.4
C.2 D.4