题目内容
10．已知e为自然对数的底数，曲线y=aex+x在点（1，ae+1）处的切线与直线2ex-y-1=0平行，则实数a=（ ）| A． | $\frac{e-1}{e}$ | B． | $\frac{2e-1}{e}$ | C． | $\frac{e-1}{2e}$ | D． | $\frac{2e-1}{2e}$ |
分析 求出函数的导数，求得切线的斜率，由两直线平行的条件：斜率相等，解方程可得a．
解答 解：y=aex+x的导数为y′=aex+1，
可得曲线y=aex+x在点（1，ae+1）处的切线斜率为ae+1，
由切线与直线2ex-y-1=0平行，可得
ae+1=2e，解得a=$\frac{2e-1}{e}$．
故选：B．
点评 本题考查导数的运用：求切线的斜率，同时考查两直线平行的条件：斜率相等，考查运算能力，属于基础题．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
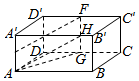已知长方体ABCD-A1B1C1D1，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$，$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$，E，F分别为AA1，C1D1中点，则$\overrightarrow{EF}$可用$\vec a，\vec b，\vec c$表示为$\frac{1}{2}$（$\overrightarrow{a}$+$\overrightarrow{c}$）+$\overrightarrow{b}$．
15．观察如图：
则第（ ）行的各数之和等于20112．
则第（ ）行的各数之和等于20112．
| A． | 2010 | B． | 2009 | C． | 1006 | D． | 1005 |
如图，四棱锥O-ABCD中，AC垂直平分BD，|$\overrightarrow{OB}$|=2，|$\overrightarrow{OD}$|=1，则（$\overrightarrow{OA}$+$\overrightarrow{OC}$）•（$\overrightarrow{OB}$-$\overrightarrow{OD}$）的值是3．
19．已知m，n，l为三条不同的直线，α，β，γ为三个不同的平面，则下列命题中正确的是（ ）
| A． | 若m⊥l，n⊥l，则m∥n | B． | 若m∥α，n∥α，则m∥n | C． | 若m⊥α，n⊥α，则m∥n | D． | 若α⊥γ，β⊥γ，则α∥β |