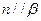题目内容
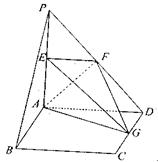
如图,在四棱锥 中,底面
中,底面 是边长为2的菱形,且
是边长为2的菱形,且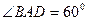 ,
,
 为正三角形,
为正三角形, 为
为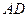 的中点,
的中点, 为棱
为棱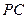 的中点
的中点
(1)求证: 平面
平面
(2)求二面角 的大小
的大小

 中,底面
中,底面 是边长为2的菱形,且
是边长为2的菱形,且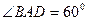 ,
, 为正三角形,
为正三角形, 为
为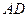 的中点,
的中点, 为棱
为棱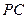 的中点
的中点(1)求证:
 平面
平面
(2)求二面角
 的大小
的大小
(1)见解析(2)arctan2
(1)设H为AC与BD的交点,连结EH,则EH为△PAC的中位线
∴EH//PA,又∵EH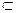 平面EBD ,PA
平面EBD ,PA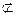 平面EBD
平面EBD
∴PA//平面EBD -------------------------------------4分
(2)∵O为AD的中点,PA=PD
∴PO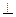 AD,又∵PO
AD,又∵PO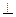 AB
AB
∴PO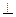 平面ABCD,连结CO交BD于Q
平面ABCD,连结CO交BD于Q
∴PO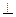 CO,过E作EF
CO,过E作EF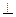 CO于F
CO于F
∴EF//PO,∴EF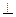 平面ABCD ----------------------------8分
平面ABCD ----------------------------8分
过F作FG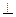 BD于G,连结GE,则EG
BD于G,连结GE,则EG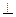 BD,
BD,
∴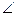 EGF为二面角E-BD-C的平面角 --------------------------10分
EGF为二面角E-BD-C的平面角 --------------------------10分
∴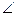 EGF="arctan2 " --------------------------12分
EGF="arctan2 " --------------------------12分
∴EH//PA,又∵EH
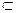 平面EBD ,PA
平面EBD ,PA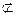 平面EBD
平面EBD∴PA//平面EBD -------------------------------------4分
(2)∵O为AD的中点,PA=PD
∴PO
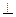 AD,又∵PO
AD,又∵PO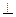 AB
AB∴PO
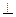 平面ABCD,连结CO交BD于Q
平面ABCD,连结CO交BD于Q∴PO
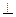 CO,过E作EF
CO,过E作EF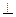 CO于F
CO于F∴EF//PO,∴EF
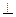 平面ABCD ----------------------------8分
平面ABCD ----------------------------8分过F作FG
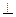 BD于G,连结GE,则EG
BD于G,连结GE,则EG BD,
BD,∴
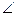 EGF为二面角E-BD-C的平面角 --------------------------10分
EGF为二面角E-BD-C的平面角 --------------------------10分∴
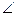 EGF="arctan2 " --------------------------12分
EGF="arctan2 " --------------------------12分
练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
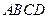 所在平面与圆
所在平面与圆 所在平面相交于
所在平面相交于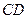 ,线段
,线段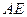 垂直于圆
垂直于圆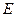 是圆
是圆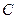 、
、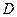 的点,
的点,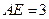 ,圆
,圆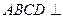 平面
平面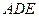 ;
;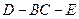 的平面角的正切值.
的平面角的正切值.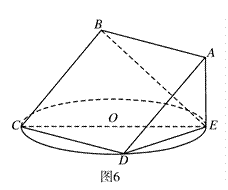
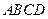 中,
中,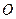 是
是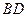 的中点,
的中点,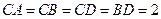 ,
,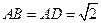 .(Ⅰ)求证:
.(Ⅰ)求证: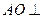 平面
平面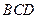 ;(Ⅱ)求异面直线
;(Ⅱ)求异面直线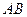 与
与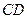 所成角的大小;
所成角的大小;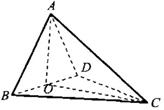
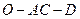 的大小.
的大小.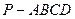 (如图)底面是边长为2的正方形.侧棱
(如图)底面是边长为2的正方形.侧棱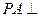 底面
底面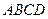 ,
,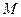 、
、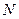 分别为
分别为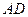 、
、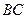 的中点,
的中点,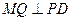 于
于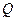 。
。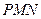 ⊥平面
⊥平面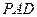 ;
;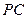 与平面
与平面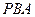 所成角的正弦值为
所成角的正弦值为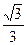 ,求PA的长;
,求PA的长;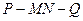 的余弦值。
的余弦值。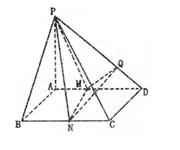
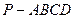 中,底面
中,底面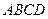 是矩形,已知
是矩形,已知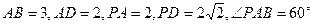 .
.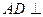 平面
平面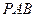 ;
;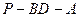 的大小.
的大小.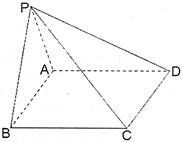
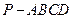 中,
中,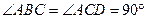 ,
,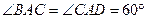 ,
,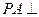 底面
底面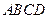 ,
,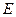 为
为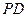 的中点,
的中点,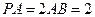 .
.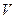 ;
;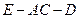 的大小.
的大小.
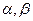 为互不重合的平面,
为互不重合的平面,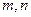 为互不重合的直线,给出下列四个命题:]
为互不重合的直线,给出下列四个命题:]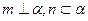 则
则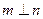 ;
;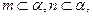
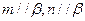 ,则
,则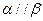 ;
;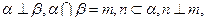 则
则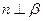
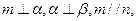 则
则