题目内容
直线kx-y=k-1与直线ky=x+2k的交点在第二象限内,则k的取值范围是 ________.
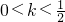
分析:把两条直线方程联立,解出交点坐标,然后利用第二象限的点横坐标小于0,纵坐标大于0,列出关于k的不等式组,求出不等式组的解集即可得到k的取值范围.
解答:联立两直线方程得
 ,由②得y=
,由②得y= ③,把③代入①得:kx-
③,把③代入①得:kx- =k-1,
=k-1,当k+1≠0即k≠-1时,解得x=
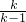 ,把x=
,把x=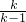 代入③得到y=
代入③得到y=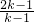 ,所以交点坐标为(
,所以交点坐标为(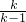 ,
,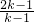 )
)因为直线kx-y=k-1与直线ky=x+2k的交点在第二象限内,
得
 解得0<k<1,k>1或k<
解得0<k<1,k>1或k< ,所以不等式组的解集为0<k<
,所以不等式组的解集为0<k<
则k的取值范围是0<k<

故答案为:0<k<

点评:本题考查学生会利用两直线方程联立得到方程组求出交点坐标,掌握第二象限点坐标的特点,会求不等式组的解集,是一道中档题.

练习册系列答案
相关题目