题目内容
(本小题满分14分)
已知抛物线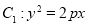 上一点
上一点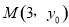 到其焦点F的距离为4;椭圆
到其焦点F的距离为4;椭圆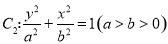 的离心率
的离心率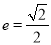 ,且过抛物线的焦点F.
,且过抛物线的焦点F.
(I)求抛物线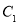 和椭圆
和椭圆 的标准方程;
的标准方程;
(II)过点F的直线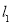 交抛物线
交抛物线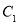 于A、B两不同点,交
于A、B两不同点,交 轴于点N,已知
轴于点N,已知 ,求证:
,求证: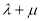 为定值.
为定值.
(III)直线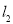 交椭圆
交椭圆 于P,Q两不同点,P,Q在x轴的射影分别为
于P,Q两不同点,P,Q在x轴的射影分别为 ,
,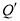 ,
,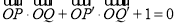 ,若点S满足:
,若点S满足: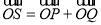 ,证明:点S在椭圆
,证明:点S在椭圆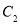 上.
上.
(I)抛物线 的方程为
的方程为 ;椭圆的标准方程为
;椭圆的标准方程为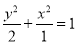 (II)见解析;(III)见解析.
(II)见解析;(III)见解析.
【解析】
试题分析:(1)设椭圆的方程,用待定系数法求出 的值;(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式
的值;(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式 :计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.
:计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.
试题解析:(Ⅰ)抛物线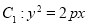 上一点
上一点 到其焦点
到其焦点 的距离为
的距离为 ;
;
抛物线的准线为
抛物线上点 到其焦点
到其焦点 的距离
的距离 等于到准线的距离
等于到准线的距离
所以 ,所以
,所以
抛物线 的方程为
的方程为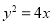 2分
2分
椭圆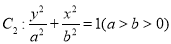 的离心率
的离心率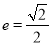 ,且过抛物线的焦点
,且过抛物线的焦点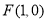
所以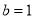 ,
,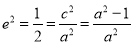 ,解得
,解得
所以椭圆的标准方程为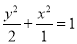 4分
4分
(Ⅱ)直线 的斜率必存在,设为
的斜率必存在,设为 ,设直线
,设直线 与椭圆
与椭圆 交于
交于
则直线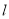 的方程为
的方程为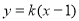 ,
, 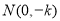
联立方程组:
所以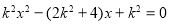
 ,所以
,所以 (*) 5分
(*) 5分
由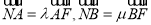 得:
得:

得:  7分
7分
所以
将(*)代入上式,得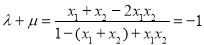 9分
9分
(Ⅲ)设
所以 ,则
,则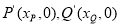
由 得
得 (1) 11分
(1) 11分
 ,(2)
,(2)  (3)
(3)
(1)+(2)+(3)得:
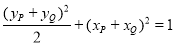
即 满足椭圆
满足椭圆 的方程
的方程
命题得证 14分
考点:椭圆的定义及其性质的应用.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
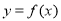 在
在 上有定义,对于任意给定正数
上有定义,对于任意给定正数 ,定义函数
,定义函数 ,
, 为
为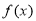 的“孪生函数”,若给定函数
的“孪生函数”,若给定函数 ,
, ,则
,则 = .
= .  ,则输出的
,则输出的

 B.
B.  C.
C.  D.
D. 
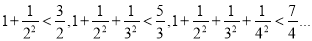 则可归纳出关于正整数
则可归纳出关于正整数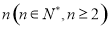 的式子为__________________.
的式子为__________________.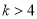 是方程
是方程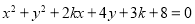 表示圆的充要条件;
表示圆的充要条件;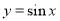 的图象向右平移
的图象向右平移 单位,再保持纵坐标不变,横坐标变为原来的
单位,再保持纵坐标不变,横坐标变为原来的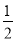 ,得到函数
,得到函数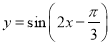 的图象;
的图象;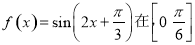 上为增函数;
上为增函数;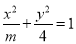 的焦距为2,则实数m的值等于5.
的焦距为2,则实数m的值等于5. 中,内角A,B,C对边分别为
中,内角A,B,C对边分别为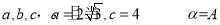 时,两直线恰好相互垂直;
时,两直线恰好相互垂直;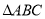 的面积
的面积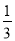 ,且各人能否通过测试是相互独立的,则至少有一位同学能通过测试的概率为
,且各人能否通过测试是相互独立的,则至少有一位同学能通过测试的概率为 B.
B. 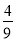 C.
C. 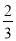 D.
D. 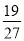
 的首项
的首项 ,前
,前 项和为
项和为 ,且满足
,且满足 ,则满足
,则满足 的
的 的最大值为
的最大值为  是奇函数,则
是奇函数,则