题目内容
动点P在抛物线y=x2+1上运动,则动点P和两定点A(-1,0)、B(0,-1)所成的△PAB的重心的轨迹方程是
9x2-3y+6x+1=0
9x2-3y+6x+1=0
.分析:利用三角形的重心坐标公式,通过坐标转化,把重心坐标转化到P代入抛物线方程即可.
解答:解:在三角形△ABC中,三个顶点坐标分别为:A(x1,y1),B(x2,y2),C(x3,y3)
则△ABC的重心坐标为:Q(
(x1+x2+x3),
(y1+y2+y3))
那么在△PAB中,设P点坐标为P(x0,y0)
设重心坐标为Q(x',y')应该有x'=
(x0-1),y'=
(y0-1).
解出x0,y0 得x0=3x'+1,y0=3y'+1
因为P(x0,y0 )在抛物线y=x2+1上则有 3y'+1=(3x'+1)2+1化简得y'=3x'2+2x'+
即△PAB的重心的轨迹方程是:y=3x2+2x+
.
即9x2-3y+6x+1=0.
故答案为:9x2-3y+6x+1=0.
则△ABC的重心坐标为:Q(
| 1 |
| 3 |
| 1 |
| 3 |
那么在△PAB中,设P点坐标为P(x0,y0)
设重心坐标为Q(x',y')应该有x'=
| 1 |
| 3 |
| 1 |
| 3 |
解出x0,y0 得x0=3x'+1,y0=3y'+1
因为P(x0,y0 )在抛物线y=x2+1上则有 3y'+1=(3x'+1)2+1化简得y'=3x'2+2x'+
| 1 |
| 3 |
即△PAB的重心的轨迹方程是:y=3x2+2x+
| 1 |
| 3 |
即9x2-3y+6x+1=0.
故答案为:9x2-3y+6x+1=0.
点评:本题考查曲线轨迹方程的求解,重心坐标公式的应用,转化思想的应用,考查计算能力.

练习册系列答案
相关题目
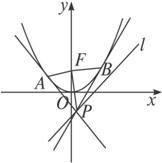
 如图,设抛物线C:y=x2的焦点为F,动点P在直线l:x-y-2=0上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.则△APB的重心G的轨迹方程为
如图,设抛物线C:y=x2的焦点为F,动点P在直线l:x-y-2=0上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.则△APB的重心G的轨迹方程为