Question

如图，设抛物线C:y=x²的焦点为F，动点P在直线l∶x-y-2=0上运动，过P作抛物线C的两条切线PA、PB，且与抛物线C分别相切于A、B两点.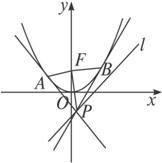

（1）求△APB的重心G的轨迹方程.

（2）证明∠PFA=∠PFB.

Answer 1

（1）解：设切点A、B坐标分别为(x,x₀²)和(x₁,x₁²)(x₁≠x₀)，

∴切线AP的方程为2x₀x-y-x₀²=0;切线BP的方程为2x₁x-y-x₁²=0.

解得P点的坐标为x_p=,y_p=x₀x₁，

所以△APB的重心G的坐标为x_G=，

y_G=.

所以y_p=-3y_G+4x_G2，由点P在直线l上运动，

从而得到重心G的轨迹方程为x-(-3y+4x²)-2=0,即y=(4x²-x+2).

（2）证明：证法1：因为=(x₀,x₀²-),=(,x₀x₁-),

=(x₁,x₁²-).由于P点在抛物线外，则||≠0. ∴cosAFP=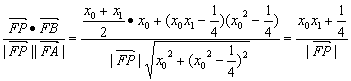,?同理有cosBFP=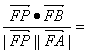

∴∠AFP=∠PFB.

证法2：①当x₁x₀=0时,由于x₁≠x₀，不妨设x₀=0，

则y₀=0,所以P点坐标为(,0)，则P点到直线AF的距离为d₁=;而直线BF的方程：y-=x,即(x₁²-)x-x₁y+x₁=0.所以P点到直线BF的距离为

d₂=.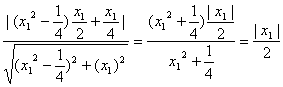

所以d₁=d₂，即得∠AFP=∠PFB.

②当x₁x₀≠0时，直线AF的方程：

y-=，即(x₀²-)x-x₀y+x₀=0.

直线BF的方程：y-=(x-0).即(x₁²-)x-x₁y+x₁=0.

所以P点到直线AF的距离为

d₁=，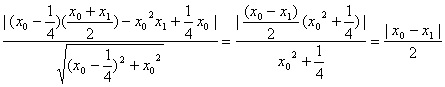

同理可得到P点到直线BF的距离

d₂=，因此由d₁=d₂，可得到∠AFP=∠PFB.