题目内容
已知曲线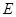 上任意一点
上任意一点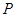 到两个定点
到两个定点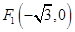 ,
,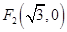 的距离之和为4.
的距离之和为4.
(1)求曲线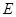 的方程;
的方程;
(2)设过(0,-2)的直线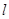 与曲线
与曲线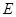 交于
交于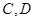 两点,且
两点,且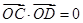 (
(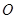 为原点),求直线
为原点),求直线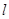 的方程.
的方程.
 上任意一点
上任意一点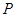 到两个定点
到两个定点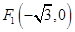 ,
,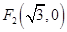 的距离之和为4.
的距离之和为4.(1)求曲线
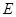 的方程;
的方程;(2)设过(0,-2)的直线
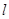 与曲线
与曲线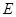 交于
交于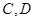 两点,且
两点,且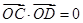 (
(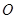 为原点),求直线
为原点),求直线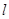 的方程.
的方程.(1)
(2)直线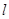 的方程是
的方程是 或
或 .
.

(2)直线
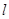 的方程是
的方程是 或
或 .
. 试题分析:(1)根据椭圆的定义,可知动点
 的轨迹为椭圆,
的轨迹为椭圆,其中
 ,
, ,则
,则 .
.所以动点
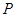 的轨迹方程为
的轨迹方程为 . 4分
. 4分(2)当直线
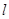 的斜率不存在时,不满足题意.
的斜率不存在时,不满足题意. 当直线
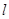 的斜率存在时,设直线
的斜率存在时,设直线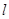 的方程为
的方程为 ,
,设
 ,
, ,
,∵
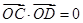 ,∴
,∴ .
.∵
 ,
, ,∴
,∴ .
.∴
 .… ①
.… ① 由方程组
 得
得 .
.则
 ,
, ,代入①,得
,代入①,得 .
. 即
 ,解得,
,解得, 或
或 . 10分
. 10分所以,直线
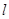 的方程是
的方程是 或
或 . 12分
. 12分点评:解决的关键是利用椭圆的定义来得到轨迹方程,这是求轨迹的首要考虑的方法之一,同时联立方程组,结合韦达定理来得到直线方程,属于基础题。

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 的左右焦点坐标分别是
的左右焦点坐标分别是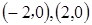 ,离心率
,离心率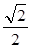 ,直线
,直线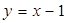 与椭圆
与椭圆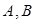 .
.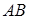 的长度.
的长度.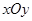 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为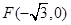 ,右顶点为
,右顶点为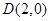 ,设点
,设点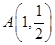 .
.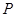 是椭圆上的动点,求线段
是椭圆上的动点,求线段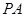 中点
中点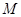 的轨迹方程;
的轨迹方程;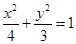 的右焦点
的右焦点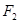 的直线交椭圆于于
的直线交椭圆于于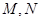 两点,令
两点,令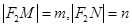 ,则
,则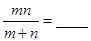 。
。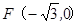 ,且过点
,且过点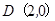 .
.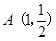 ,若
,若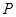 是椭圆上的动点,求线段
是椭圆上的动点,求线段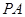 的中点
的中点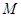 的轨迹方程.
的轨迹方程. 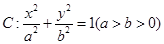 的离心率为
的离心率为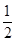 ,且过点
,且过点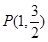 ,
,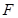 为其右焦点.
为其右焦点.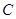 的方程;
的方程; 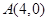 的直线
的直线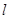 与椭圆相交于
与椭圆相交于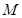 、
、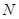 两点(点
两点(点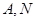 两点之间),若
两点之间),若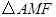 与
与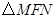 的面积相等,试求直线
的面积相等,试求直线 与抛物线
与抛物线 的焦点均在
的焦点均在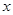 轴上,
轴上,



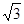






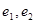 ;
;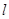 与椭圆
与椭圆 ,且
,且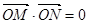 (其中
(其中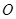 坐标原点),请问是否存在这样的直线
坐标原点),请问是否存在这样的直线 若存在,求出直线
若存在,求出直线 ,
, 是椭圆
是椭圆 的两个焦点,点
的两个焦点,点 在椭圆上,且
在椭圆上,且 ,则△
,则△ 的面积为 .
的面积为 . 是曲线
是曲线 上的点,
上的点, ,则( )
,则( )


