题目内容
10.不等式x2+ax+b<0的解集是(-1,3),则( )| A. | $\left\{\begin{array}{l}{a=2}\\{b=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=-2}\\{b=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=1}\\{b=-6}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=3}\\{b=2}\end{array}\right.$ |
分析 根据一元二次不等式与对应方程的关系,利用根与系数的关系式,即可求出a、b的值.
解答 解:∵不等式x2+ax+b<0的解集是(-1,3),
∴对应方程x2+ax+b=0的两个实数根为-1和3,
由根与系数的关系,得
-1+3=-a,且-1×3=b;
∴a=-2,b=-3.
故选:B.
点评 本题考查了一元二次不等式与对应方程的关系应用问题,也考查了根与系数关系的应用问题,是基础题目.

练习册系列答案
相关题目
2.定义在R上的偶函数f(x)满足f(x+2)=f(x),且在区间[-3,-2]上是减函数,若A,B是锐角三角形的两个内角,且A>B,则( )
| A. | f(sinA)>f(cosB) | B. | f(sinA)<f(cosB) | C. | f(sinA)>f(sinB) | D. | f(cosA)>f(cosB) |
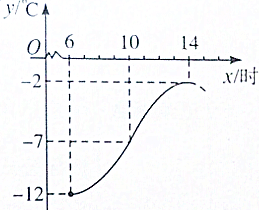 如图,牡丹江市某天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,|φ<π|).
如图,牡丹江市某天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,|φ<π|).