题目内容
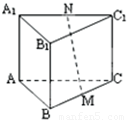
如图，正三棱柱的九条棱都相等，三个侧面都是正方体，M、N分别是BC和A1C1的中点，求MN与CC1所成角的余弦值．
解：设正三棱柱的棱长为a，取AC中点O，连接MO，NO，则NO垂直平面ABC
∴∠MNO为MN与CC1所成的角
在Rt△MNO中，∠NOM=90°，NO=A1A=2a
∵M，O分别为BC，AC的中点，∴MO=
AB=a
∴MN=
=
a
∴cos∠MNO=
=
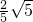
分析：取AC中点O，连接MO，NO，则NO垂直平面ABC，可得∠MNO为MN与CC1所成的角，在Rt△MNO中，即可求得MN与CC1所成角的余弦值．
点评：本题考查空间角，考查学生的计算能力，正确作出空间角是关键．
∴∠MNO为MN与CC1所成的角
在Rt△MNO中，∠NOM=90°，NO=A1A=2a
∵M，O分别为BC，AC的中点，∴MO=
AB=a∴MN=
=a∴cos∠MNO=
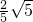
=分析：取AC中点O，连接MO，NO，则NO垂直平面ABC，可得∠MNO为MN与CC1所成的角，在Rt△MNO中，即可求得MN与CC1所成角的余弦值．
点评：本题考查空间角，考查学生的计算能力，正确作出空间角是关键．
练习册系列答案
相关题目
如图，正三棱柱的九条棱都相等，三个侧面都是正方体，M、N分别是BC和A1C1的中点，求MN与CC1所成角的余弦值．
的九条棱长均为2，点P是线段
上一动点（包含点A，
），D是BC的中点．
（如图1）；
－B的正切值（如图1）；
⊥平面
（如图2）；
－B的正切值的取值范围（不必写推算过程）
