题目内容
已知正三棱柱ABC－
的九条棱长均为2，点P是线段
上一动点（包含点A，
），D是BC的中点．
（Ⅰ）求证AD⊥平面
（如图1）；
（Ⅱ）求二面角A－
－B的正切值（如图1）；
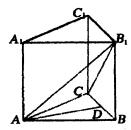
图1
（Ⅲ）确定点P的位置，使平面
⊥平面
（如图2）；
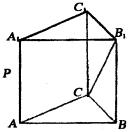
图2
（Ⅳ）指出二面角P－
－B的正切值的取值范围（不必写推算过程）
答案：
解析：
解析：
（Ⅰ）证明：如答图1，∵  ，∴  ，又平面 ，
交线为 （Ⅱ）解：如答图1，作 由（Ⅰ）及三垂线定理，得
答图1 （Ⅲ）解：如答图2， ∵ 同理 ∴ 平面 （Ⅳ）
答图2 |
，
，∴ 
交
于
，连
，
，∴ 
为二面角
—
—
的平面角
，
，∴ 
为
的中点，连结
交
于
，连
，则
，∴ 
，∴ 
，又
，
，
练习册系列答案
相关题目
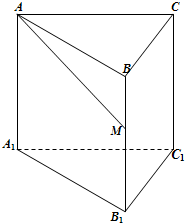如图，已知正三棱柱ABC-A1B1C1的底面边长为1，高为h（h＞2），动点M在侧棱BB1上移动．设AM与侧面BB1C1C所成的角为θ．
已知正三棱柱ABC-A1B1C1的每条棱长均为a，M为棱A1C1上的动点．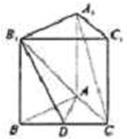
如图，已知正三棱柱ABC-A1B1C1中，D是BC的中点，AA1=AB=1．
（2009•湖北模拟）如图，已知正三棱柱ABC-A1B1C1各棱长都为a，P为棱A1B上的动点．