题目内容

如图所示，正三棱柱ABC—A1B1C1的九条棱长均为2a,D、E分别为BC、CC1的中点，B1D交BE于F，过F作AB1的垂线交AB1于G.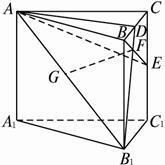

（1）证明AD⊥BE；

（2）求异面直线BE和AB1的距离.

（1）证明：由正三棱柱性质得△ABC为正三角形，且面ABC⊥面BB1C1C，交线为BC.?

∵D是BC中点，∴AD⊥面BB1C1C.?

∴AD⊥BE.?

（2）解析：∵AD⊥面BB1C1C，∴AB1在侧面BB1C1C上的射影是DB1.?

∵BB1C1C是正方形,E、D是CC1、BC中点，∴BE⊥B1D.∴AB1⊥BE.?

又∵AD⊥BE，AD∩AB1=A，?

∴BE⊥面AB1D.∴BE⊥GF于F.?

又∵FG⊥AB1于G，∴FG是BE与AB1的公垂线段.?

在正方形BB1C1C中，BF⊥DB1于F，由射影定理知DF·DB1=BD2.?

∴DF=.?

又在Rt△ADB1中，△FGB1∽△ADB1,∴.??

∴FG=.?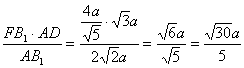

∴BE与AB1的距离为.


练习册系列答案
相关题目
如图所示，正三棱柱ABC-A1B1C1的底面边长是2，侧棱长是
3
，D是AC的中点．
（Ⅰ）求证：B1C∥平面A1BD；
（Ⅱ）求二面角A1-BD-A的大小；
（Ⅲ）求点A到平面A1BD的距离．

（08年唐山一中调研二） 如图所示，正三棱柱的底面边长为a，点M在BC上，是以点M为直角顶点的等腰直角三角形。

   （Ⅰ）求证：点M为边BC的中点；

   （Ⅱ）求点C到平面的距离；

   （Ⅲ）求二面角的大小。

 
如图所示，正三棱柱ABC-A1B1C1的棱长均为a，D、E分别为C1C与AB的中点，A1B交AB1于G。

（1）求证：A1B⊥AD；
（2）求证：CE∥平面AB1D。
如图所示，正三棱柱ABC-A1B1C1的底面边长是2，侧棱长是，D是AC的中点．
（Ⅰ）求证：B1C∥平面A1BD；
（Ⅱ）求二面角A1-BD-A的大小；
（Ⅲ）求点A到平面A1BD的距离．
如图所示，正三棱柱ABC-A1B1C1的底面边长是2，侧棱长是，D是AC的中点．
（Ⅰ）求证：B1C∥平面A1BD；
（Ⅱ）求二面角A1-BD-A的大小；
（Ⅲ）求点A到平面A1BD的距离．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网