题目内容
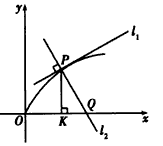
设直线l1与曲线
相切于点P，直线l2过点P 且垂直于l1，若l2交x轴于Q点，又作PK垂直于x轴于点K，求KQ的长。
相切于点P，直线l2过点P 且垂直于l1，若l2交x轴于Q点，又作PK垂直于x轴于点K，求KQ的长。 解：如图：设P（x0，y0）
即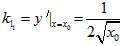
∵直线l1与l2垂直，则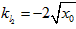
∴直线l2的方程为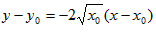
，
∵点P（x0，y0）在曲线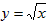
上，
∴
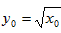
在直线l2的方程中令y=0，即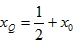
又xK=x0，
∴
。
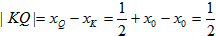即
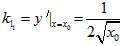
∵直线l1与l2垂直，则
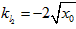
∴直线l2的方程为
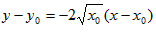， ∵点P（x0，y0）在曲线
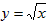上，∴
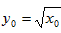
在直线l2的方程中令y=0，即
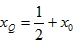
又xK=x0，
∴
。
练习册系列答案
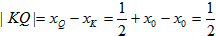新思维寒假作业系列答案
相关题目
相切于P，直线l2过P且垂直于l1，若l2交x轴于Q点，又作PK垂直于x轴于K，求KQ的长.
相切于P，直线l2过P且垂直于l1,若l2交x轴于Q点,又作PK垂直于x轴于K点,求KQ的长.
相切于点P，直线l2过点P且垂直于l1.若l2交x轴于Q点，又作PK垂直于x轴于K，求KQ的长.
相切于点P,直线l2过点P且垂直于l1,若l2交x轴于点Q,又作PK垂直于x轴于K,求KQ的长.