题目内容
已知△ABC是等腰三角形,∠C=90°,AB=4,则 等于
等于
- A.-8
- B.
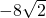
- C.8
- D.
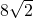
A
分析:根据所给的条件看出三角形是一个直角三角形,根据三角函数的定义做出直角边的长度,看出两个向量的夹角,利用数量积的定义做出结果.
解答:∵△ABC是等腰三角形,∠C=90°,AB=4,
∴三角形是一个等腰直角三角形,
直角边长是
两个向量的夹角是180°-45°=135°
∴ =2
=2 =-8
=-8
故选A.
点评:本题考查平面向量的数量积,本题解题的关键是根据所给的条件看出两个向量的夹角,这是一个易错题,出错的原因是把三角形第一个内角当成向量的夹角.
分析:根据所给的条件看出三角形是一个直角三角形,根据三角函数的定义做出直角边的长度,看出两个向量的夹角,利用数量积的定义做出结果.
解答:∵△ABC是等腰三角形,∠C=90°,AB=4,
∴三角形是一个等腰直角三角形,
直角边长是

两个向量的夹角是180°-45°=135°
∴
 =2
=2 =-8
=-8故选A.
点评:本题考查平面向量的数量积,本题解题的关键是根据所给的条件看出两个向量的夹角,这是一个易错题,出错的原因是把三角形第一个内角当成向量的夹角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 .其中正确结论的序号是________.(写出全部正确结论的序号)
.其中正确结论的序号是________.(写出全部正确结论的序号) .其中正确结论的序号是 .(写出全部正确结论的序号)
.其中正确结论的序号是 .(写出全部正确结论的序号)