题目内容
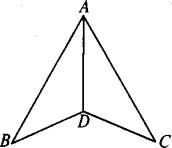
已知△ABC是等腰直角三角形，AB=AC=a，AD是斜边BC上的高，以AD为折痕使∠BDC成直角．在折起后形成的三棱锥A-BCD中，有如下三个结论：①直线AD⊥平面BCD；②侧面ABC是等边三角形；③三棱锥A-BCD的体积是
．其中正确结论的序号是________．（写出全部正确结论的序号）
①、②、③
分析：由△ABC是等腰直角三角形，AB=AC=a，AD是斜边BC上的高，折起后，根据线面垂直的判定定理可判断①的真假；由等腰三角形的判定，可知②的真假；根据棱锥体积公式求出三棱锥A-BCD的体积可以判断③的真假．进而得到答案．
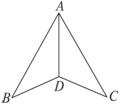
解答：以AD为折痕使∠BDC成直角，所得图形如下图所示：
由AD⊥BD，AD⊥CD，易得：①直线AD⊥平面BCD，正确；
由AB=AC，可得②侧面ABC是等边三角形，正确；
由BD=AD=CD=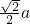
，可得③三棱锥A-BCD的体积是，正确．
故答案为：①、②、③
点评：本题考查的知识点是棱锥的结构特征，线面垂直的判定，棱锥的体积，其中根据对折后，AD与BD与CD的垂直关系不变，AB，AC的相等关系不变，是解答的关键．
分析：由△ABC是等腰直角三角形，AB=AC=a，AD是斜边BC上的高，折起后，根据线面垂直的判定定理可判断①的真假；由等腰三角形的判定，可知②的真假；根据棱锥体积公式求出三棱锥A-BCD的体积可以判断③的真假．进而得到答案．
解答：以AD为折痕使∠BDC成直角，所得图形如下图所示：
由AD⊥BD，AD⊥CD，易得：①直线AD⊥平面BCD，正确；
由AB=AC，可得②侧面ABC是等边三角形，正确；
由BD=AD=CD=
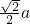，可得③三棱锥A-BCD的体积是，正确．故答案为：①、②、③
点评：本题考查的知识点是棱锥的结构特征，线面垂直的判定，棱锥的体积，其中根据对折后，AD与BD与CD的垂直关系不变，AB，AC的相等关系不变，是解答的关键．
练习册系列答案
相关题目
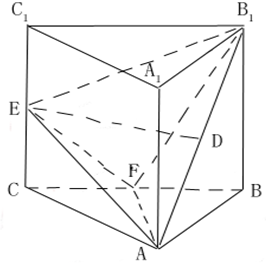如图，已知直三棱柱ABC-A1B1C1中，△ABC是等腰直角三角形，∠BAC=90°，且AB=AA1，D、E、F分别是B1A、CC1、BC的中点．现设A1A=2a
（2013•丽水一模）已知直三棱柱ABC-A1B1C1，底面△ABC是等腰三角形，∠BAC=120°，
