题目内容
已知动点P,Q都在曲线C: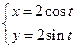 
(t为参数)上,对应参数分别为t=
与t=2 (0<<2π),M为PQ的中点.
(1)求M的轨迹的参数方程;
(2)将M到坐标原点的距离d表示为的函数,并判断M的轨迹是否过坐标原点.
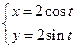(t为参数)上,对应参数分别为t=与t=2 (0<<2π),M为PQ的中点.(1)求M的轨迹的参数方程;
(2)将M到坐标原点的距离d表示为
的函数,并判断M的轨迹是否过坐标原点.(1)
(2)见解析．
(2)见解析．
（1）依题意有P(2cos,2sin),Q(2cos2,2sin2),
因此M(cos+cos2,sin+sin2).所以M的轨迹的参数方程为
(为参数,0<<2π).
(2)M点到坐标原点的距离d=
=
(0<<2π).
当=π时,d=0,故M的轨迹过坐标原点.
,2sin),Q(2cos2,2sin2),因此M(cos
+cos2,sin+sin2).所以M的轨迹的参数方程为(为参数,0<<2π).(2)M点到坐标原点的距离d=
= (0<<2π).当
=π时,d=0,故M的轨迹过坐标原点.
练习册系列答案
计算高手系列答案
相关题目
表示的曲线是（ ）
，则直线的斜率为 .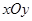
中，曲线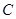
的参数方程为
(
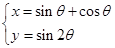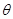为参数)，若以直角坐标系
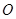点为极点，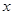
轴正方向为极轴，且长度单位相同，建立极坐标系，得直线
的极坐标方程为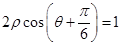
．求直线
＝1上找一点，使这一点到直线x－2y－12＝0的距离最小．
（
为参数且
）与曲线
(
是参数且
)，则直线
与曲线
的交点坐标为 . 
上有3个不同的点到曲线
的距离等于2，则
.
，5）对应的点的直角坐标是 。
(
为参数)化为普通方程是（ ）
