题目内容
已知
，
，则以下结论中，正确的有________（填入所有正确结论的编号）．
①
； ②β=kπ（k∈Z）； ③
．
①②
分析：直接根据两角差的正切公式即可判断出①成立，再根据①成立可得结论②成立，最后把②代入，根据终边相同的角对应的三角函数值相等可以判断出③不成立．
解答：∵tan（β+
）=tan[（α+β）-（α-）]
=
=
=1．即①成立；
∴由得：β+=kπ+?β=kπ，k∈Z．即②成立；
∴tan（α+β）=tan（α+kπ）=tanα=
?α=kπ+arctan．即③不成立．
所以，只有①②为正确结论．
故答案为：①②．
点评：本题主要考查两角差的正切公式的应用以及终边相同的角对应的三角函数值相等这一结论的应用．解决问题的关键在于由已知条件得到①成立．
分析：直接根据两角差的正切公式即可判断出①成立，再根据①成立可得结论②成立，最后把②代入
，根据终边相同的角对应的三角函数值相等可以判断出③不成立．解答：∵tan（β+
）=tan[（α+β）-（α-）]=
=
=1．即①成立；∴由
得：β+=kπ+?β=kπ，k∈Z．即②成立；∴tan（α+β）=tan（α+kπ）=tanα=
?α=kπ+arctan．即③不成立．所以，只有①②为正确结论．
故答案为：①②．
点评：本题主要考查两角差的正切公式的应用以及终边相同的角对应的三角函数值相等这一结论的应用．解决问题的关键在于由已知条件得到①成立．
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
已知 Q（x）是幂函数，则以下结论中正确的一个是（ ）
| A、Q（x）在区间（0，+∞）上总是增函数． | B、Q（x）的图象总过点（1，1） | C、Q（x）的值域一定是实数集R | D、Q（x）一定是奇函数或者偶函数 |
、
是两个不共线的向量，O是同一平面内的一个定点，
，则以下结论中，错误的是
.
.
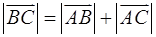D.以上选项A、B、C不全对
，
，则以下结论中，正确的有 （填入所有正确结论的编号）．
； ②β=kπ（k∈Z）； ③
．