题目内容
已知f（x）=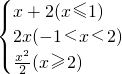
且f（a）=3，求a的值．
解：①当a≤1时，f（a）=a+2，
由a+2=3，得a=1，与a≤-1相矛盾，应舍去．
②当-1＜a＜2时，f（a）=2a，
由2a=3，得a=
，满足-1＜a＜2．
③当a≥2时，f（a）=
，
由=3，得a=±
，又a≥2，∴a=．
综上可知，a的值为或．
分析：根据分段函数的分段标准进行分类讨论，分别求解每一段的方程，将符合条件的值找出即可．
点评：本题主要考查了分段函数求值的问题，以及分类讨论的数学思想，属于基础题．
由a+2=3，得a=1，与a≤-1相矛盾，应舍去．
②当-1＜a＜2时，f（a）=2a，
由2a=3，得a=
，满足-1＜a＜2．③当a≥2时，f（a）=
，由
=3，得a=±，又a≥2，∴a=．综上可知，a的值为
或．分析：根据分段函数的分段标准进行分类讨论，分别求解每一段的方程，将符合条件的值找出即可．
点评：本题主要考查了分段函数求值的问题，以及分类讨论的数学思想，属于基础题．
练习册系列答案
相关题目
已知f（x）满足f（x+4）=f（x）且f（4+x）=f（4-x），若2≤x≤6时，f（x）=|x-b|+c，f（4）=2，则f（lnb）与f（lnc）的大小关系是（ ）
| A、f（lnb）≤f（lnc） | B、f（lnb）≥f（lnc） | C、f（lnb）＞f（lnc） | D、f（lnb）＜f（lnc） |