题目内容
设椭圆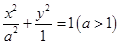 的左、右焦点分别为
的左、右焦点分别为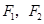 ,
,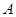 是椭圆上位于
是椭圆上位于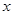 轴上方的动点
(Ⅰ)当
轴上方的动点
(Ⅰ)当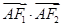 取最小值时,求
取最小值时,求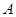 点的坐标;
点的坐标;
(Ⅱ)在(Ⅰ)的情形下,是否存在以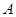 为直角顶点的内接于椭圆的等腰直角三角形?若存在,求出共有几个;若不存在,请说明理由.
为直角顶点的内接于椭圆的等腰直角三角形?若存在,求出共有几个;若不存在,请说明理由.
【答案】
解:(Ⅰ)设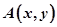 ,
,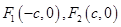 ,则
,则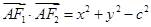
因为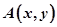 在椭圆上,所以
在椭圆上,所以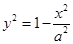 ,
,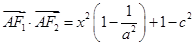
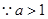 ,当
,当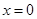 时,
时,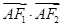 取得最小值,此时
取得最小值,此时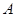 点的坐标为
点的坐标为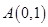 .
.
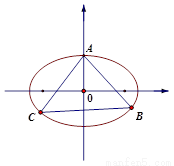 (Ⅱ)设两个顶点为B,C,显然直线AC斜率存在,不妨设AC的直线方程为
(Ⅱ)设两个顶点为B,C,显然直线AC斜率存在,不妨设AC的直线方程为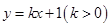 ,代入椭圆的方程
,代入椭圆的方程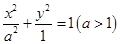 中可得
中可得 ,解得
,解得 (即A点的横坐标),
(即A点的横坐标),
由弦长公式得:
同理: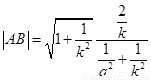 z
z
由 ,即
,即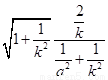
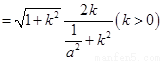 ,化解得:
,化解得:
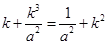 ,即
,即 .
.
考虑关于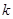 的方程
的方程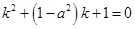 ,其判别式
,其判别式
(1)当 时,
时, ,其两根设为
,其两根设为 ,由于
,由于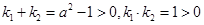 ,故两根必为正根,显然
,故两根必为正根,显然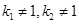 ,故关于
,故关于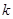 的方程
的方程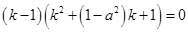 有三解,相应地,这样的等腰直角三角形有三个.
有三解,相应地,这样的等腰直角三角形有三个.
(2)当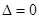 时,
时,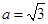 ,此时方程
,此时方程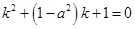 的解
的解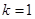 ,故方程
,故方程
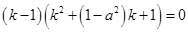 只有一解,相应地,这样的等腰直角三角形只有一个.
只有一解,相应地,这样的等腰直角三角形只有一个.
(3)当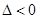 时,显然方程只有
时,显然方程只有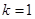 这一个解,相应地,这样的等腰直角三角形只有一个.
这一个解,相应地,这样的等腰直角三角形只有一个.
综上:当 时,这样的等腰直角三角形有三个;当
时,这样的等腰直角三角形有三个;当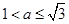 时,这样的等腰直角三角形只有一个.
时,这样的等腰直角三角形只有一个.
【解析】略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 的左、右焦点分别是F1、F2,离心率
的左、右焦点分别是F1、F2,离心率 ,右准线l上的两动点M、N,且
,右准线l上的两动点M、N,且 ,
, ,求a、b的值;
,求a、b的值; 最小时,求证
最小时,求证 与
与 共线。
共线。 
 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线y=x+2相切.
,以原点为圆心,椭圆的短半轴长为半径的圆与直线y=x+2相切.