题目内容
【题目】设![]() ,
,![]() ,
,![]() ,给出以下四种排序:①M,N,T;②M,T,N;③N,T,M;④T,N,M.从中任选一个,补充在下面的问题中,解答相应的问题.
,给出以下四种排序:①M,N,T;②M,T,N;③N,T,M;④T,N,M.从中任选一个,补充在下面的问题中,解答相应的问题.
已知等比数列![]() 中的各项都为正数,
中的各项都为正数,![]() ,且__________依次成等差数列.
,且__________依次成等差数列.
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)设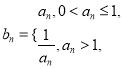 数列
数列![]() 的前n项和为
的前n项和为![]() ,求满足
,求满足![]() 的最小正整数n.
的最小正整数n.
注:若选择多种排序分别解答,按第一个解答计分.
【答案】(Ⅰ)答案见解析;(Ⅱ)答案见解析.
【解析】
(Ⅰ)根据选的条件求出等比数列![]() 的公比,写出其通项公式即可;
的公比,写出其通项公式即可;
(Ⅱ)由(Ⅰ)得出数列![]() 的通项公式,然后利用等比数列前
的通项公式,然后利用等比数列前![]() 项和
项和![]() 解不等式,再由
解不等式,再由![]() 确定其最小值.
确定其最小值.
解:(解答一)选②或③:
(Ⅰ)设![]() 的公比为q,则
的公比为q,则![]() .由条件得
.由条件得![]() ,
,
又因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
解得![]() (负值舍去).所以
(负值舍去).所以![]() .
.
(Ⅱ)由题意得![]() ,则
,则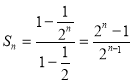 .由
.由![]() 得
得
![]() ,即
,即![]() ,又因为
,又因为![]() ,所以n的最小值为7.
,所以n的最小值为7.
(解答二)选①或④:
(Ⅰ)设![]() 的公比为q,则
的公比为q,则![]() .由条件得
.由条件得![]() ,
,
又因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
解得![]() (负值舍去).所以
(负值舍去).所以![]() .
.
(Ⅱ)由题意得![]() ,则
,则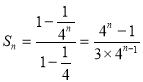 .由
.由![]() 得
得
![]() ,即
,即![]() ,又因为
,又因为![]() ,所以n的最小值为5.
,所以n的最小值为5.

练习册系列答案
相关题目