题目内容
(1)若(2)若![]() (
(![]() -ax-b)=0,求a,b的值.
-ax-b)=0,求a,b的值.
分析:(1)x→2时,分式的分母x2-x-2→0,同时分母中有因式x-2,又由于分式的极限值是常数2,因此分子中也应有因式x-2,需约去公因式x-2后,其极限值才有可能是常数.
(2)需通分才能求解.
解:(1)令x2+ax+b=(x-2)(x+c),则
x2+ax+b=x2+(c-2)x-2c,a=c-2,b=-2c.
于是
原式=![]()
![]() =
=![]()
![]() =
=![]() ,
,
∴![]() =2.
=2.
解得 c=4.∴a=2,b=-8.
(2)原式可化为![]() (
(![]() -
-![]() )=0,
)=0,
即![]()
![]() =0,
=0,
![]()
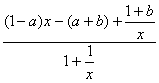 =0.
=0.
因为![]()
![]() =0,
=0,![]()
![]() =0,且原式极限为0,所以应有
=0,且原式极限为0,所以应有
![]() ∴a=1,b=-1.
∴a=1,b=-1.

练习册系列答案
相关题目
 。
。 ,求a的值;
,求a的值; 是偶函数,若过点A(1,m)
是偶函数,若过点A(1,m) 可作曲线y=f(x)的三条切线,求实数m的范围。
可作曲线y=f(x)的三条切线,求实数m的范围。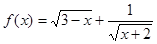 的定义域为集合A,
的定义域为集合A,
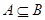 ,求a的取值范围;
,求a的取值范围; ,a=
,a= ,求
,求 .
. 。
。 ,求a的值 .(2)若
,求a的值 .(2)若 ,求a的值.
,求a的值.