题目内容
15．下列各进制数中，最小的是（ ）| A． | 1002（3） | B． | 210（6） | C． | 1000（4） | D． | 111111（2） |
分析 利用累加权重法，将四个答案中的数均转化为十进制的数，进而比较可得答案．
解答 解：1002（3）=2+1×27=29
210（6）=2×36+1×6=78
1000（4）=43=64
111111（2）=26-1=63
故选：A．
点评 本题考查的知识点是不同进制之间的转换，其中其它进制转为十进制方法均为累加数字×权重，十进制转换为其它进制均采用除K求余法．
练习册系列答案
相关题目
10．执行如图所示的程序框图，若输出的值为-105，则输入的n的值可能是（ ）
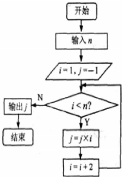
| A． | 5 | B． | 7 | C． | 8 | D． | 10 |
20．
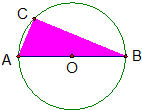如图，点C为半径是1的圆上一点，且劣弧长AC是劣弧长CB的一半，假设你在这个图形上随机地撒一粒豆子，则∠ABC及豆子落在阴影区域的概率分别是（ ）
如图，点C为半径是1的圆上一点，且劣弧长AC是劣弧长CB的一半，假设你在这个图形上随机地撒一粒豆子，则∠ABC及豆子落在阴影区域的概率分别是（ ）| A． | $\frac{π}{6}$，$\frac{\sqrt{3}}{2π}$ | B． | $\frac{π}{3}$，$\frac{\sqrt{3}}{2π}$ | C． | $\frac{π}{6}$，$\frac{\sqrt{3}}{2}$ | D． | $\frac{π}{6}$，$\frac{3}{2π}$ |
7．
公司随机抽取M名员工作为样本，得到这M名员工参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：
（Ⅰ）求出表中M和图中a的值；
（Ⅱ）若该公司员工有240人，试估计员工参加社区服务的次数在区间[10，15）内的人数；
（Ⅲ）在所取样本中，从参加社区服务的次数不少于20次的员工中任选2人，求至多一人参加社区服务次数在区间[25，30）内的概率．
公司随机抽取M名员工作为样本，得到这M名员工参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：（Ⅰ）求出表中M和图中a的值；
（Ⅱ）若该公司员工有240人，试估计员工参加社区服务的次数在区间[10，15）内的人数；
（Ⅲ）在所取样本中，从参加社区服务的次数不少于20次的员工中任选2人，求至多一人参加社区服务次数在区间[25，30）内的概率．
| 分组 | 频数 | 频率 |
| [10，15） | 10 | 0.25 |
| [15，20） | 24 | n |
| [20，25） | m | p |
| [25，30） | 2 | 0.05 |
| 合计 | M | 1 |
4．已知函数f（x）=2lnx+1在点（1，f（1））处的切线为l，点（an，an+1）在l上，且a1=2，则a2015=（ ）
| A． | 22014-1 | B． | 22014+1 | C． | 22015-1 | D． | 22015+1 |
5．已知i是虚数单位，m是实数，若$\frac{m+i}{2-i}$是纯虚数，则m=（ ）
| A． | -2 | B． | -$\frac{1}{2}$ | C． | 2 | D． | $\frac{1}{2}$ |