题目内容
已知曲线E:ax2+by2=1(a>0,b>0),经过点M 的直线l与曲线E交于点A、B,且
的直线l与曲线E交于点A、B,且 =-2
=-2 .
.
(1)若点B的坐标为(0,2),求曲线E的方程;
(2)若a=b=1,求直线AB的方程.
 的直线l与曲线E交于点A、B,且
的直线l与曲线E交于点A、B,且 =-2
=-2 .
.(1)若点B的坐标为(0,2),求曲线E的方程;
(2)若a=b=1,求直线AB的方程.
(1)x2+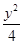 =1(2)y=
=1(2)y= x-1.
x-1.
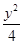 =1(2)y=
=1(2)y= x-1.
x-1.(1)设A(x0,y0),由已知B(0,2),M( ,0),所以
,0),所以 =
= ,
, =(x0-
=(x0- ,y0).
,y0).
由于 =-2
=-2 ,所以(-
,所以(- ,2)=-2(x0-
,2)=-2(x0- ,y0),所以
,y0),所以 即A(
即A( ,-1),将A、B点的坐标代入曲线E的方程,得
,-1),将A、B点的坐标代入曲线E的方程,得 解得
解得
所以曲线E的方程为x2+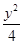 =1.
=1.
(2)当a=b=1时,曲线E为圆x2+y2=1,设A(x1,y1),B(x2,y2).又 =-2
=-2 ,
,
所以 =-2(x1-
=-2(x1- ,y1),
,y1),
即有
 +
+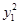 =1①,
=1①, +
+ =1②,由①×4-②,得(2x1+x2)(2x1-x2)=3,所以2x1-x2=
=1②,由①×4-②,得(2x1+x2)(2x1-x2)=3,所以2x1-x2= ,解得x1=
,解得x1= ,x2=0.由x1=
,x2=0.由x1= ,得y1=±
,得y1=±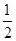 .当A
.当A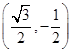 时,B(0,-1),此时kAB=-
时,B(0,-1),此时kAB=- ,直线AB的方程为y=-
,直线AB的方程为y=- x+1;
x+1;
当A 时,B(0,1),此时kAB=
时,B(0,1),此时kAB= ,直线AB的方程为y=
,直线AB的方程为y= x-1.
x-1.
 ,0),所以
,0),所以 =
= ,
, =(x0-
=(x0- ,y0).
,y0).由于
 =-2
=-2 ,所以(-
,所以(- ,2)=-2(x0-
,2)=-2(x0- ,y0),所以
,y0),所以 即A(
即A( ,-1),将A、B点的坐标代入曲线E的方程,得
,-1),将A、B点的坐标代入曲线E的方程,得 解得
解得
所以曲线E的方程为x2+
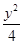 =1.
=1.(2)当a=b=1时,曲线E为圆x2+y2=1,设A(x1,y1),B(x2,y2).又
 =-2
=-2 ,
,所以
 =-2(x1-
=-2(x1- ,y1),
,y1),即有

 +
+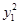 =1①,
=1①, +
+ =1②,由①×4-②,得(2x1+x2)(2x1-x2)=3,所以2x1-x2=
=1②,由①×4-②,得(2x1+x2)(2x1-x2)=3,所以2x1-x2= ,解得x1=
,解得x1= ,x2=0.由x1=
,x2=0.由x1= ,得y1=±
,得y1=±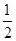 .当A
.当A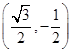 时,B(0,-1),此时kAB=-
时,B(0,-1),此时kAB=- ,直线AB的方程为y=-
,直线AB的方程为y=- x+1;
x+1;当A
 时,B(0,1),此时kAB=
时,B(0,1),此时kAB= ,直线AB的方程为y=
,直线AB的方程为y= x-1.
x-1.
练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 是离心率为
是离心率为 的椭圆
的椭圆 :
:
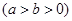 上的一点,斜率为
上的一点,斜率为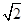 的直线
的直线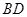 交椭圆
交椭圆 ,
,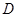 两点,且
两点,且 、
、
 ,
, 的斜率之和为定值.
的斜率之和为定值. ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线 的焦点.
的焦点.
 APQ=
APQ= 为椭圆
为椭圆 右焦点,圆
右焦点,圆 与椭圆
与椭圆 的一个公共点为
的一个公共点为 ,且直线
,且直线 与圆
与圆 相切与点
相切与点 。
。
 的值及椭圆
的值及椭圆 满足
满足 ,其中
,其中 是椭圆
是椭圆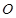 为原点,直线
为原点,直线 与
与 的斜率之积为
的斜率之积为 ,求证:
,求证: 为定值。
为定值。 的双曲线和离心率为
的双曲线和离心率为 的椭圆有相同的焦点
的椭圆有相同的焦点 、
、 ,
, 是两曲线的一个公共点,若
是两曲线的一个公共点,若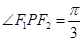 ,则
,则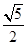
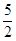


 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,其左焦点到点P(2,1)的距离为
,其左焦点到点P(2,1)的距离为 .不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.
.不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.
 =1(a>b>0),称圆心在原点O、半径是
=1(a>b>0),称圆心在原点O、半径是 的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为F(
的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为F( ,0),其短轴的一个端点到点F的距离为
,0),其短轴的一个端点到点F的距离为 .
. ·
· 的取值范围;
的取值范围; =1(a>b>0)的左、右焦点,点M在x轴上,且
=1(a>b>0)的左、右焦点,点M在x轴上,且 =
=
 ,过点F2的直线与椭圆交于A、B两点,且AM⊥x轴,
,过点F2的直线与椭圆交于A、B两点,且AM⊥x轴, ·
·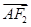 =0.
=0.
 ,求椭圆的方程.
,求椭圆的方程. 的右准线方程是 .
的右准线方程是 .