题目内容
顶点在原点,焦点在x轴上的抛物线截直线2x-y+1=0所得的弦长为
解:设所求抛物线方程为y2=ax(a≠0),直线与抛物线交于A、B两点,A(x1,y1)、B(x2,y2),由 得4x2+(4-a)x+1=0.
得4x2+(4-a)x+1=0.
∴x1+x2=![]() ,x1·x2=
,x1·x2=![]() .
.
∴|AB|=![]() |x1-x2|
|x1-x2|
=![]()
![]() =
=![]() .
.
解得a=12或-4.
又由Δ=(4-a)2-4×4=a2-8a>0,得a<0或a>8.
∴a=12或a=-4都适合.故所求抛物线方程为y2=12x或y2=-4x.

练习册系列答案
相关题目

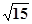 。求抛物线的方程.
。求抛物线的方程. ,求抛物线的方程.
,求抛物线的方程.