Question

实数k为何值时,复数z=(k2-3k-4)+(k2-5k-6)i分别是(1)实数;(2)虚数;(3)纯虚数;(4)零?

Answer 1

分析：根据复数的分类,弄清一个复数满足什么条件分别为实数、虚数、纯虚数,分清复数的实部、虚部.

解：(1)当k²-5k-6=0,即k=6或k=-1时,复数z为实数.

(2)当k²-5k-6≠0,即k≠6且k≠-1时,复数z为虚数.

(3)当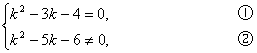

由①得k=4或k=-1.

由②得k≠6且k≠-1,

∴当k=4时,z为纯虚数.

(4)当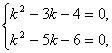即k=-1时,z=0.

绿色通道

    由复数z的实部、虚部的取值来确定复数z是实数、虚数、纯虚数.在解题时关键是确定z的实部、虚部,并要注意纯虚数的概念满足两条:实部为零,虚部不为零.