题目内容
在△ABC内任取一点P则△ABP与△ABC的面积之比大于
的概率是( )
| 2 |
| 3 |
分析:作出与AB平行,且到AB的距离等于C到AB距离的
的线段DE,如图所示.根据三角形面积公式,可得当点P位于△ADE内部时,△ABP与△ABC的面积之比大于
.由此利用相似三角形的性质与几何概型公式,即可算出△ABP与△ABC的面积之比大于
的概率.
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
解答:解: 分别在AC、BC上取点,使AD=
分别在AC、BC上取点,使AD=
AC且AE=
BC,连结DE.
∵
=
=
,
∴DE∥BC,且DE到AB的距离等于点C到AB距离的
.
因此当点P在△ABC内且在DE的上方时,S△ABP>
S△ABC,
即点P位于△ADE内部时,△ABP与△ABC的面积之比大于
.
根据几何概型公式,可得所求概率等于△ADE的面积与△ABC的面积之比.
∵DE∥BC,
=
=
,
∴△ADE∽△ABC,可得
=(
)2=
,
因此,△ABP与△ABC的面积之比大于
的概率P=
.
故选:C
 分别在AC、BC上取点,使AD=
分别在AC、BC上取点,使AD=| 2 |
| 3 |
| 2 |
| 3 |
∵
| AD |
| AC |
| BE |
| BC |
| 2 |
| 3 |
∴DE∥BC,且DE到AB的距离等于点C到AB距离的
| 2 |
| 3 |
因此当点P在△ABC内且在DE的上方时,S△ABP>
| 2 |
| 3 |
即点P位于△ADE内部时,△ABP与△ABC的面积之比大于
| 2 |
| 3 |
根据几何概型公式,可得所求概率等于△ADE的面积与△ABC的面积之比.
∵DE∥BC,
| CD |
| CA |
| CE |
| CB |
| 1 |
| 3 |
∴△ADE∽△ABC,可得
| S△ADE |
| S△ABC |
| CD |
| CA |
| 1 |
| 9 |
因此,△ABP与△ABC的面积之比大于
| 2 |
| 3 |
| 1 |
| 9 |
故选:C
点评:本题在△ABC内取一点P,求△ABP与△ABC的面积之比大于
的概率.着重考查了相似三角形的性质三角形面积公式与几何概型的计算等知识,属于中档题.
| 2 |
| 3 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
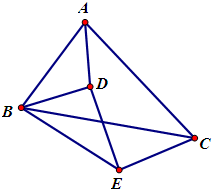 已知:在△ABC内任取一点D,连接AD,BD,点E在△ABC外,∠EBC=∠ABD,∠ECB=∠DAB,求证:△DBE∽△ABC.
已知:在△ABC内任取一点D,连接AD,BD,点E在△ABC外,∠EBC=∠ABD,∠ECB=∠DAB,求证:△DBE∽△ABC.