题目内容
1.若直线$\frac{x}{a}$+$\frac{y}{b}$=1通过点P(cosθ,sinθ),则下列不等式正确的是( )| A. | a2+b2≤1 | B. | a2+b2≥1 | C. | $\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$≤1 | D. | $\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$≥1 |
分析 先把点代入得到bcosθ+asinθ=ab,即可得到$\sqrt{{a}^{2}+{b}^{2}}$(sinθ+φ)=ab,得到$\sqrt{{a}^{2}+{b}^{2}}$≤ab,问题得以判断
解答 解:直线$\frac{x}{a}$+$\frac{y}{b}$=1通过点P(cosθ,sinθ),
∴bcosθ+asinθ=ab,
∴$\sqrt{{a}^{2}+{b}^{2}}$sin(θ+φ)=ab,其中tanφ=$\frac{b}{a}$,
∴$\sqrt{{a}^{2}+{b}^{2}}$≥ab,
∴a2+b2≥a2b2,
∴$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$≥1,
故选:D
点评 本题考查了直线和点的位置关系以及三角函数的问题,属于中档题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
11.-2log510-log50.25+2=( )
| A. | 0 | B. | -1 | C. | -2 | D. | -4 |
12.等差数列{an}前n项和为Sn,${S_p}=\frac{p}{q}$,${S_q}=\frac{q}{p}$(p≠q),则Sp+q的值是( )
| A. | 大于4 | B. | 小于4 | C. | 等于4 | D. | 不确定 |
6.设θ是两个非零向量$\overrightarrow{a}$、$\overrightarrow{b}$的夹角,若对任意实数t,|$\overrightarrow{a}$+t$\overrightarrow{b}$|的最小值为1,则下列判断正确的是( )
| A. | 若|$\overrightarrow{a}$|确定,则θ唯一确定 | B. | 若|$\overrightarrow{b}$|确定,则θ唯一确定 | ||
| C. | 若θ确定,则|$\overrightarrow{b}$|唯一确定 | D. | 若θ确定,则|$\overrightarrow{a}$|唯一确定 |
11.曲线$\left\{\begin{array}{l}x=5cosθ\\ y=4sinθ\end{array}$(θ为参数)的焦点到双曲线x2-$\frac{y^2}{2}$=1的渐近线的距离为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{10}$ |
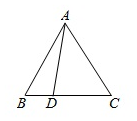 如图,在△ABC中,若AB=AC=3,cos∠BAC=$\frac{1}{2}$,$\overrightarrow{DC}$=2$\overrightarrow{BD}$,则$\overrightarrow{AD}•\overrightarrow{BC}$=$-\frac{3}{2}$.
如图,在△ABC中,若AB=AC=3,cos∠BAC=$\frac{1}{2}$,$\overrightarrow{DC}$=2$\overrightarrow{BD}$,则$\overrightarrow{AD}•\overrightarrow{BC}$=$-\frac{3}{2}$.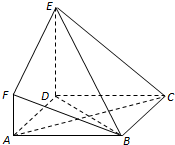 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF=3$\sqrt{6}$.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF=3$\sqrt{6}$.