题目内容
已知函数 ,
,
 在
在 上为增函数,且
上为增函数,且 ,求解下列各题:
,求解下列各题:
(1)求 的取值范围;
的取值范围;
(2)若 在
在 上为单调增函数,求
上为单调增函数,求 的取值范围;
的取值范围;
(3)设 ,若在
,若在 上至少存在一个
上至少存在一个 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
【答案】
(1) ;(2)
;(2) ;
(3)
;
(3)
【解析】
试题分析:(1) 在
在 上为增函数,则
上为增函数,则 在
在 上恒成立,即
上恒成立,即 在
在 上恒成立.由于分母恒大于0,故
上恒成立.由于分母恒大于0,故 在
在 上恒成立,而这只需
上恒成立,而这只需 的最小值
的最小值 即可.由此可得
即可.由此可得 的取值范围;
的取值范围;
(2) 在
在 上为单调增函数,则其导数大于等于0在
上为单调增函数,则其导数大于等于0在 恒成立,变形得
恒成立,变形得 在
在 恒成立.与(1)题不同的是,这里不便求
恒成立.与(1)题不同的是,这里不便求 的最小值,故考虑分离参数,即变形为
的最小值,故考虑分离参数,即变形为 .这样只需
.这样只需 大于等于
大于等于 的最大值即可.而
的最大值即可.而 ,所以
,所以 ;
;
(3)构造新函数 =
= ,这样问题转化为:在
,这样问题转化为:在 上至少存在一个
上至少存在一个 ,使得
,使得 成立,求
成立,求 的取值范围.而这只要
的取值范围.而这只要 的最大值大于0即可.
的最大值大于0即可.
试题解析:(1)∵ 在
在 上为增函数
上为增函数
∴ 在
在 上恒成立,即
上恒成立,即 在
在 上恒成立
上恒成立
又
∴ 在
在 上恒成立
2分
上恒成立
2分
只须 ,即
,即 ,由
,由 有
有 3分
3分
 ∴
∴ 4分
4分
(2)由(1)问得


 在
在 上为单调增函数
上为单调增函数
 在
在 恒成立
6分
恒成立
6分
∴ 即
即 ,而
,而
 在
在 恒成立时有
恒成立时有 ,即函数
,即函数 在
在 上为单调增函数时,
上为单调增函数时, 的范围为
的范围为 ;
8分
;
8分
(3)由(1)问可知 ,
, ,
,
可以构造新函数 =
= 10分
10分
①.当 时,
时, ,
,
所以在 上不存在一个
上不存在一个 ,使得
,使得 成立. 11分
成立. 11分
②.当 时,
时,
∵ ∴
∴ ,
, ,所以
,所以 在
在 恒成立.
恒成立.
故 在
在 上单调递增,
上单调递增,
∴只需满足 ,解得
,解得 13分
13分
故 的取值范围是
的取值范围是 14分
14分
考点:1、导数的应用;2、不等式关系.

练习册系列答案
相关题目
 ,
,
 在
在 上为增函数,且
上为增函数,且 ,求解下列各题:
,求解下列各题: 的取值范围;
的取值范围; 在
在 上为单调增函数,求
上为单调增函数,求 的取值范围;
的取值范围; ,若在
,若在 上至少存在一个
上至少存在一个 ,使得
,使得 成立,求
成立,求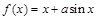 .
.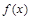 在
在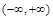 上为增函数,求实数a的取值范围;
上为增函数,求实数a的取值范围;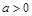 时,设
时,设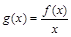 ,求
,求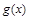 在
在 上的最大值和最小值.
上的最大值和最小值.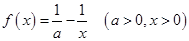
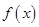 在上为增函数
在上为增函数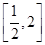 上的值域为
上的值域为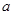 的值。
的值。