题目内容
某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本y(万元)与年产量x(吨)之间的函数关系式可以近似地表示为y=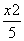 -48x+8 000,已知此生产线年产量最大为210吨.
-48x+8 000,已知此生产线年产量最大为210吨.
(1)求年产量为多少吨时,生产每吨产品的平均成本最低,并求最低成本;
(2)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?
解析: (1)每吨平均成本为 (万元).
(万元).
则 =
= +
+ -48≥2
-48≥2  -48=32,
-48=32,
当且仅当 =
= ,即x=200时取等号.
,即x=200时取等号.
∴年产量为200吨时,每吨平均成本最低为32万元.
(2)设年获得总利润为R(x)万元,
则R(x)=40x-y=40x-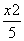 +48x-8 000
+48x-8 000
=-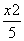 +88x-8 000=-
+88x-8 000=- (x-220)2+1 680(0≤x≤210).
(x-220)2+1 680(0≤x≤210).
∵R(x)在[0,210]上是增函数,
∴x=210时,R(x)有最大值为
- (210-220)2+1 680=1 660.
(210-220)2+1 680=1 660.
∴年产量为210吨时,可获得最大利润1 660万元.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目


 元
元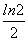 D.ln 2
D.ln 2