题目内容
已知 ,且
,且 .
.
(1)求tanα的值;
(2)当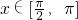 时,求函数f(x)的最小值.
时,求函数f(x)的最小值.
解:(1) 所以
所以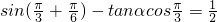 ,
,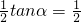 所以tanα=1;
所以tanα=1;
(2)由(1)得: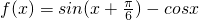 =
= =sin(x-
=sin(x- ),
),
因为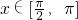 所以x-
所以x-
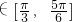 ,sin(x-
,sin(x- )
) ;
;
当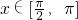 时,函数f(x)的最小值为:
时,函数f(x)的最小值为: .
.
分析:(1)直接利用 求出tanα的值.
求出tanα的值.
(2)利用(1)的结果,化简函数的表达式为一个角的一个三角函数的形式,根据x的范围,求出函数的最小值.
点评:本题是基础题,考查三角函数的化简求值,三角函数的最值的求法,考查计算能力,常考题型.
 所以
所以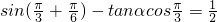 ,
,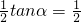 所以tanα=1;
所以tanα=1;(2)由(1)得:
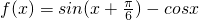 =
= =sin(x-
=sin(x- ),
),因为
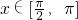 所以x-
所以x-
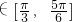 ,sin(x-
,sin(x- )
) ;
;当
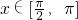 时,函数f(x)的最小值为:
时,函数f(x)的最小值为: .
.分析:(1)直接利用
 求出tanα的值.
求出tanα的值.(2)利用(1)的结果,化简函数的表达式为一个角的一个三角函数的形式,根据x的范围,求出函数的最小值.
点评:本题是基础题,考查三角函数的化简求值,三角函数的最值的求法,考查计算能力,常考题型.

练习册系列答案
相关题目
 (2012•徐州模拟)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,
(2012•徐州模拟)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答, ,函数
,函数 ·
·
 的最小正周期T及单调减区间
的最小正周期T及单调减区间 分别是△ABC内角A,B,C的对边,其中A为锐角,
分别是△ABC内角A,B,C的对边,其中A为锐角, 且
且 ,求A,b和△ABC的面积S
,求A,b和△ABC的面积S