题目内容
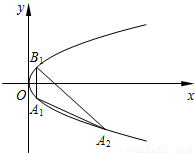
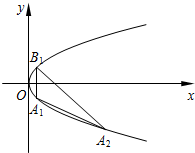 如图A1(x1,y1)(y1<0)是抛物线y2=mx(m>0)上的点,作点A1关于x轴的对称点B1,过B1作与抛物线在A1处的切线平行的直线B1A2交抛物线于点A2.
如图A1(x1,y1)(y1<0)是抛物线y2=mx(m>0)上的点,作点A1关于x轴的对称点B1,过B1作与抛物线在A1处的切线平行的直线B1A2交抛物线于点A2.(1)若A1(4,-4),求点A2的坐标;
(2)若△A1A2B1的面积为16,且在A1,B1两点处的切线互相垂直.
①求抛物线方程;
②作A2关于x轴的对称点B2,过B2作与抛物线在A2处的切线平行的直线B2A3,交抛物线于点A3,…,如此继续下去,得一系列点A4,A5,…,设An(xn,yn),求满足xn≥10000x1的最小自然数n.
分析:(1)由A1(4,-4)在抛物线上代入可求m,设出A2(x2,-2x2),对函数y=-
求导根据导数的几何意义可求x2,即可求解A2.
(2)①设A1,B1处切线的斜率分别为K1,K2,容易得出K1•K2=-1,代入点的坐标即可得到m与x1 的方程,再设A2,结合已知又可得x2,x1的关系,代入三角形的面积公式中即可可求知x1,m,从而可求抛物线方程
②由题意可求xn与xn-1的递推关系,结合等比数列的通项公式可求n的最小值
| mx |
(2)①设A1,B1处切线的斜率分别为K1,K2,容易得出K1•K2=-1,代入点的坐标即可得到m与x1 的方程,再设A2,结合已知又可得x2,x1的关系,代入三角形的面积公式中即可可求知x1,m,从而可求抛物线方程
②由题意可求xn与xn-1的递推关系,结合等比数列的通项公式可求n的最小值
解答:解:(1)若A1(4,-4)在抛物线上
∴16=4m
∴m=4,
设A2(x2,-2x2),y=-
,y′=-
,B(4,4)
∴
=
∴x2=36
∴A2(36,-12)….….…(3分)
(2)①设A1,B1处切线的斜率分别为K1,K2,K1•K2=-1
∴(-
).
=-1
∴m=4x1 ①
设A2(x2,-
)
∴
=-
∴x2=9x1 ②
又S=
×2
(x2-x1)=16 ③由①②③知x1=1,m=4
∴抛物线方程为y2=4x…..…(6分)
②由(2)知
=-
,
∴xn=9xn-1,
∴数列{xn}为等比数列,
∴x19n-1≥10000x1
∴n≥6∴n最小值为6…(10分)
∴16=4m
∴m=4,
设A2(x2,-2x2),y=-
| mx |
| ||
2
|
∴
2
| ||
| x2-4 |
| 1 |
| 2 |
∴x2=36
∴A2(36,-12)….….…(3分)
(2)①设A1,B1处切线的斜率分别为K1,K2,K1•K2=-1
∴(-
| ||
2
|
| ||
2
|
∴m=4x1 ①
设A2(x2,-
| mx2 |
∴
-
| ||||
| x2-x1 |
| 1 | ||
2
|
∴x2=9x1 ②
又S=
| 1 |
| 2 |
| mx1 |
∴抛物线方程为y2=4x…..…(6分)
②由(2)知
-
| ||||
| xn-xn-1 |
| ||
2
|
∴xn=9xn-1,
∴数列{xn}为等比数列,
∴x19n-1≥10000x1
∴n≥6∴n最小值为6…(10分)
点评:本题主要考查了由抛物线的性质求解抛物线的方程,还考查了一定的逻辑推理与运算的能力

练习册系列答案
相关题目


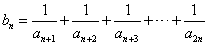 ,若对任意正整数n,当m∈[-1,1]时,不等式t2-mt+
,若对任意正整数n,当m∈[-1,1]时,不等式t2-mt+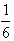 >bn恒成立,求实数t的取值范围。
>bn恒成立,求实数t的取值范围。