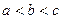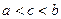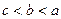题目内容
(本小题共12分) 给定函数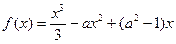 和
和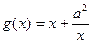
(I)求证: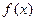 总有两个极值点;
总有两个极值点;
(II) 若
若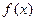 和
和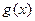 有相同的极值点,求
有相同的极值点,求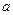 的值.
的值.
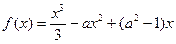 和
和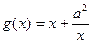
(I)求证:
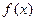 总有两个极值点;
总有两个极值点;(II)
 若
若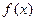 和
和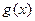 有相同的极值点,求
有相同的极值点,求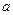 的值.
的值.证明: (I)因为
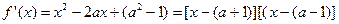 ,
,令
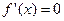 ,则
,则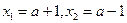 ,---------------------2分
,---------------------2分则当
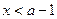 时,
时, 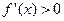 ,当
,当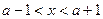 ,
, 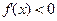
所以
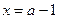 为
为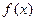 的一个极大值点, ------------4分
的一个极大值点, ------------4分同理可证
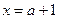 为
为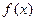 的一个极小值点.----- ----------5分
的一个极小值点.----- ----------5分另解:(I)因为
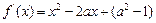 是一个二次函数,
是一个二次函数,且
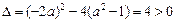 ,-------------------------------------2分
,-------------------------------------2分
所以导函数有两个不同的零点,
 又因为导函数是一个二次函数,
又因为导函数是一个二次函数,所以函数
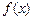 有两个不同的极值点.-------- ----------5分
有两个不同的极值点.-------- ----------5分(II) 因为
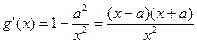 ,
,令
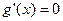 ,则
,则 ---------------6分
---------------6分因为
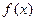 和
和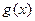 有相同的极值点, 且
有相同的极值点, 且 和
和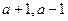 不可能相等,
不可能相等,所以当
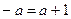 时,
时, 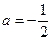 , 当
, 当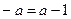 时,
时, 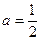 ,
,经检验,
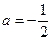 和
和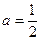 时,
时,  都是
都是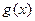 的极值点
的极值点略

练习册系列答案
相关题目
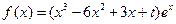 ,
,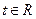 .
.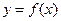 依次在
依次在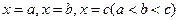 处取到极值.
处取到极值.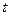 的取值范围;
的取值范围;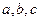 成等差数列,求
成等差数列,求 .
.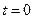 时
时 ,对任意的
,对任意的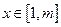 ,不等式
,不等式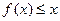 恒成立.求正整数
恒成立.求正整数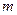 的最大值.
的最大值. 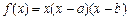 .
.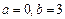 ,函数
,函数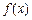 在
在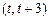 上既能取到极大值,又能取到极小值,求
上既能取到极大值,又能取到极小值,求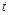 的取值范围;
的取值范围;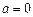 时,
时,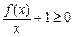 对
对 任意的
任意的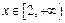 恒成立,求
恒成立,求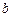 的取值范围.
的取值范围.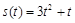 . 我们计算在
. 我们计算在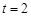 的附近区间
的附近区间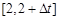 内的平均速度
内的平均速度 ,当
,当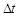 趋近于0时,平均速度
趋近于0时,平均速度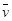 趋近于确定的值,即瞬时速度,由此可得到
趋近于确定的值,即瞬时速度,由此可得到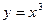 +2在
+2在
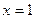 处的切线方程是 ______ ________.
处的切线方程是 ______ ________.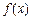 与
与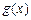 是定义在同一区间
是定义在同一区间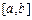 上的两个函数,若对任意
上的两个函数,若对任意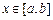 ,都有
,都有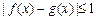 成立,则称
成立,则称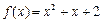 与
与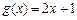 在
在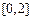
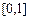
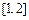
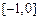
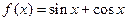 在点
在点 处的切线方程为
处的切线方程为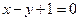
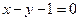
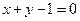
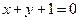
 ,则
,则 等于( )
等于( )  2
2

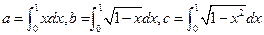 ,则
,则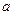 ,
,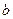 ,
, 的大小关系是( )
的大小关系是( )