题目内容
19.偶函数y=f(x)满足下列条件①x≥0时,f(x)=x3;②对任意x∈[t,t+1],不等式f(x+t)≥8f(x)恒成立,则实数t的取值范围是( )| A. | (-∞,-$\frac{3}{4}$] | B. | [-$\frac{3}{4},0$] | C. | [-2,$\frac{3}{4}$] | D. | [-$\frac{4}{3},1$] |
分析 根据f(x)为偶函数便可得到f(|x+t|)≥8f(|x|),从而有|x+t|3≥8|x|3,从而得到|x+t|≥2|x|,两边平方便有(x+t)2≥4x2,经整理便可得到3x2-2tx-t2≤0在[t,t+1]上恒成立,这样只需3(t+1)2-2t(t+1)-t2≤0,解该不等式即可得出实数t的取值范围.
解答 解:根据条件得:f(|x+t|)≥8f(|x|);
∴(|x+t|)3≥8(|x|)3;
∴(|x+t|)3≥(2|x|)3;
∴|x+t|≥2|x|;
∴(x+t)2≥4x2;
整理得,3x2-2tx-t2≤0在[t,t+1]上恒成立;
设g(x)=3x2-2tx-t2,g(t)=0;
∴g(t+1)=3(t+1)2-2t(t+1)-t2≤0;
解得t$≤-\frac{3}{4}$;
∴实数t的取值范围为(-∞,-$\frac{3}{4}$].
故选:A.
点评 考查偶函数的定义,y=x3的单调性,不等式的性质,并需熟悉二次函数的图象.

练习册系列答案
相关题目
6.|2x|<6表示的区间是( )
| A. | (3,+∞) | B. | [-3,3] | C. | (-3,3) | D. | (-∞,3) |
11.已知函数$f(x)=\frac{4x}{{3{x^2}+3}}$,函数$g(x)=\frac{1}{3}a{x^3}-{a^2}x(a≠0)$,若对任意x1∈[0,2],总存在x2∈[0,2],使f(x1)=g(x2),则实数a的取值范围是( )
| A. | (0,+∞) | B. | $[\frac{1}{3},1]$ | C. | $[\frac{1}{3},+∞)$ | D. | (0,1] |
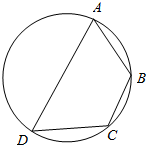 如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1.现有以下结论:
如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1.现有以下结论: