题目内容
7.在边长为1的正三角形ABC中,$\overrightarrow{BC}=2\overrightarrow{BD}$,$\overrightarrow{CA}=λ\overrightarrow{CE}$,若$\overrightarrow{AD}•\overrightarrow{BE}=-\frac{1}{4}$,则λ的值为3.分析 由$\overrightarrow{BC}=2\overrightarrow{BD}$确定点D是BC的中点,根据向量加法、减法、数乘运算,用$\overrightarrow{AB}$、$\overrightarrow{AC}$表示出$\overrightarrow{AD}$和$\overrightarrow{BE}$,由条件和数量积的运算化简$\overrightarrow{AD}•\overrightarrow{BE}$=$-\frac{1}{4}$,即可求出λ的值.
解答 解:由题意画出图象如右图: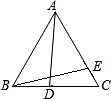
∵$\overrightarrow{BC}=2\overrightarrow{BD}$,
∴D为BC的中点,则$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),
∵$\overrightarrow{CA}=λ\overrightarrow{CE}$,
∴$\overrightarrow{CE}$=$\frac{1}{λ}$$\overrightarrow{CA}$=-$\frac{1}{λ}$$\overrightarrow{AC}$,
∴$\overrightarrow{BE}$=$\overrightarrow{AE}$-$\overrightarrow{AB}$=$\overrightarrow{CE}$-$\overrightarrow{CA}$-$\overrightarrow{AB}$=(1-$\frac{1}{λ}$)$\overrightarrow{AC}$-$\overrightarrow{AB}$,
∵$\overrightarrow{AD}•\overrightarrow{BE}$=$-\frac{1}{4}$,
∴$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)[(1-$\frac{1}{λ}$)$\overrightarrow{AC}$-$\overrightarrow{AB}$]=-$\frac{1}{4}$,
∴(1-$\frac{1}{λ}$)$\overrightarrow{AB}$$•\overrightarrow{AC}$-${\overrightarrow{AB}}^{2}$+(1-$\frac{1}{λ}$)${\overrightarrow{AC}}^{2}$-$\overrightarrow{AC}•\overrightarrow{AB}$=-$\frac{1}{2}$,
∴(-$\frac{1}{λ}$)$\overrightarrow{AB}$$•\overrightarrow{AC}$-${\overrightarrow{A{B}^{\;}}}^{2}$+(1-$\frac{1}{λ}$)${\overrightarrow{AC}}^{2}$=$-\frac{1}{2}$,
∴(-$\frac{1}{λ}$)×1×1×$\frac{1}{2}$-1+(1-$\frac{1}{λ}$)=$-\frac{1}{2}$,
解得λ=3,
故答案为:3.
点评 本题考查向量的数量积的运算,以及向量加法、减法、数乘运算及其几何意义,属于中档题.

 星级口算天天练系列答案
星级口算天天练系列答案| A. | (-∞,-$\frac{3}{4}$] | B. | [-$\frac{3}{4},0$] | C. | [-2,$\frac{3}{4}$] | D. | [-$\frac{4}{3},1$] |
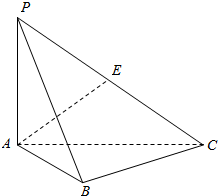 己知三棱锥P-ABC,PA⊥底面ABC,PA=AB=BC=2,直线PC与平面ABC所成的角为arctan$\frac{\sqrt{2}}{2}$.
己知三棱锥P-ABC,PA⊥底面ABC,PA=AB=BC=2,直线PC与平面ABC所成的角为arctan$\frac{\sqrt{2}}{2}$.