题目内容
已知函数
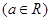 ,
,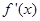 为
为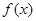 的导数.
的导数.
(1)当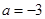 时,求
时,求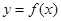 的单调区间和极值;
的单调区间和极值;
(2)设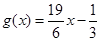 ,是否存在实数
,是否存在实数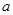 ,对于任意的
,对于任意的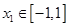 ,存在
,存在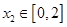 ,使得
,使得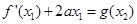 成立?若存在,求出
成立?若存在,求出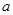 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.

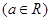 ,
,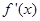 为
为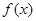 的导数.
的导数.(1)当
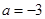 时,求
时,求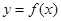 的单调区间和极值;
的单调区间和极值;(2)设
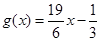 ,是否存在实数
,是否存在实数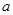 ,对于任意的
,对于任意的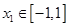 ,存在
,存在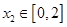 ,使得
,使得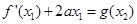 成立?若存在,求出
成立?若存在,求出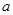 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.(1)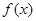 在
在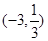 单调递减,在
单调递减,在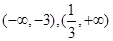 单调递增,
单调递增,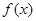 极大=
极大=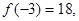
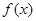 极小=
极小=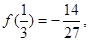
(2)存在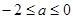 符合要求
符合要求
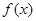 在
在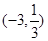 单调递减,在
单调递减,在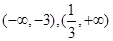 单调递增,
单调递增,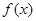 极大=
极大=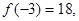
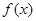 极小=
极小=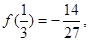
(2)存在
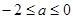 符合要求
符合要求试题分析:(1)当
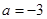 时,
时,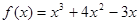 ,
,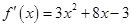 ,
,令
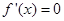 得:
得: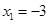 、
、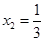 , ……2分
, ……2分所以
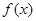 在
在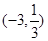 单调递减,在
单调递减,在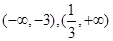 单调递增, ……4分
单调递增, ……4分所以
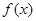 极大=
极大=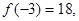
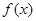 极小=
极小=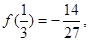 ……6分
……6分(2)在
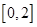 上
上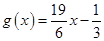 是增函数,故对于
是增函数,故对于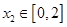 ,
,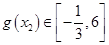 .
.设
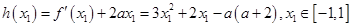 .
.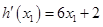 ,
,由
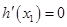 ,得
,得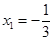 . ……8分
. ……8分 要使对于任意的
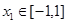 ,存在
,存在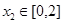 使得
使得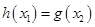 成立,只需在
成立,只需在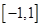 上,
上,-
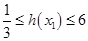 ,
, 在
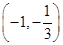 上
上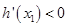 ;在
;在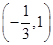 上
上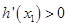 ,
,所以
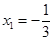 时,
时,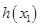 有极小值
有极小值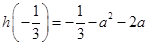 ……10分
……10分 又
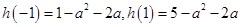 ,
,因为在
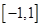 上
上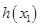 只有一个极小值,故
只有一个极小值,故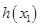 的最小值为
的最小值为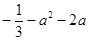 ……12分
……12分 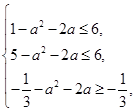 解得
解得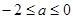 . ……14分
. ……14分 点评:导数是研究函数性质的主要依据,研究性质时一定不要忘记考虑函数的定义域.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
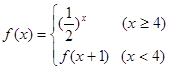 则
则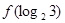 的值为 .
的值为 .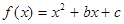 ,且
,且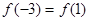 .则( )
.则( )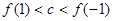
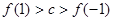

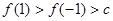
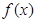 在R上是单调函数,且满足对任意
在R上是单调函数,且满足对任意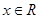 ,都有
,都有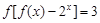 ,若则
,若则 的值是( )
的值是( )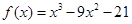 ,且
,且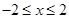 ,则
,则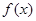 的最大值为 .
的最大值为 .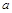 ,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的
,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的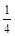 ,已知到今年为止,森林剩余面积为原来的
,已知到今年为止,森林剩余面积为原来的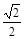 .
.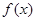 是偶函数,它在
是偶函数,它在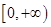 上是减函数,且
上是减函数,且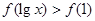 ,则x的取值范围是( )
,则x的取值范围是( )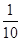 ,1)
,1)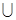 (1,
(1,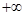 )
)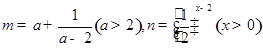 ,则
,则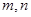 之间的大小关系是
之间的大小关系是 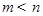
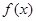 在定义域上是奇函数,且在
在定义域上是奇函数,且在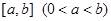 上是减函数,图像如图所示.
上是减函数,图像如图所示.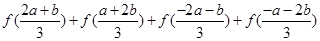 ;
;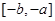 上的图像;
上的图像;