题目内容
设函数f(x)=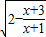 的定义域为A,不等式(x-a-1)(2a-x)>0(a<1)的解集为B.
的定义域为A,不等式(x-a-1)(2a-x)>0(a<1)的解集为B.(1)求A;
(2)若B∩A=B,求实数a的取值范围.
【答案】分析:(1)由根式内部的代数式大于等于0求解分式不等式得到集合A;
(2)求解一元二次不等式化简集合B,利用B∩A=B得到B是A的子集,然后利用端点值间的关系列不等式求解a的取值范围.
解答:解:(1)由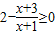 ,得
,得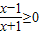 ,
,
∴x<-1或x≥1,即A=(-∞,-1)∪[1,+∞);
(2)由(x-a-1)(2a-x)>0(a<1),得(x-a-1)(x-2a)<0(a<1).
∵a<1,∴a+1>2a,∴B=(2a,a+1).
∵B∩A=B,∴B⊆A,∴2a≥1或a+1≤-1,即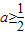 或a≤-2.
或a≤-2.
而a<1,∴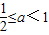 或a≤-2.
或a≤-2.
故当B∩A=B时,实数a的取值范围是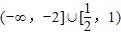 .
.
点评:本题考查了一元二次不等式的解法,考查了交集及其运算,解答的关键再于对端点值的取舍,是中档题.
(2)求解一元二次不等式化简集合B,利用B∩A=B得到B是A的子集,然后利用端点值间的关系列不等式求解a的取值范围.
解答:解:(1)由
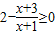 ,得
,得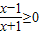 ,
,∴x<-1或x≥1,即A=(-∞,-1)∪[1,+∞);
(2)由(x-a-1)(2a-x)>0(a<1),得(x-a-1)(x-2a)<0(a<1).
∵a<1,∴a+1>2a,∴B=(2a,a+1).
∵B∩A=B,∴B⊆A,∴2a≥1或a+1≤-1,即
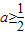 或a≤-2.
或a≤-2.而a<1,∴
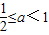 或a≤-2.
或a≤-2.故当B∩A=B时,实数a的取值范围是
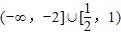 .
.点评:本题考查了一元二次不等式的解法,考查了交集及其运算,解答的关键再于对端点值的取舍,是中档题.

练习册系列答案
相关题目
