��Ŀ����
����Ŀ��ij�ؿ����г�����Ⱦ��������һ������ȥ�ۼ����д���.�ݲ�����ÿ����![]() ����λ��ȥ�ۼ����������ͷŵ�Ũ��
����λ��ȥ�ۼ����������ͷŵ�Ũ��![]() ����λ������/������������ʱ��
����λ������/������������ʱ��![]() ��λ�������仯�ĺ�����ϵʽ������Ϊ
��λ�������仯�ĺ�����ϵʽ������Ϊ
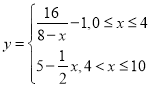 ,�������������ijһʱ�̿����е�ȥ�ۼ�Ũ��Ϊÿ��Ͷ�ŵ�ȥ�ۼ�����Ӧʱ�����ͷŵ�Ũ��֮��. ��ʵ��֪����������ȥ�ۼ���Ũ�Ȳ�����
,�������������ijһʱ�̿����е�ȥ�ۼ�Ũ��Ϊÿ��Ͷ�ŵ�ȥ�ۼ�����Ӧʱ�����ͷŵ�Ũ��֮��. ��ʵ��֪����������ȥ�ۼ���Ũ�Ȳ�����![]() ������/��������ʱ����������ȥ������.
������/��������ʱ����������ȥ������.
��1����һ������![]() ����λ��ȥ�ۼ�����ȥ��ʱ��ɴX����
����λ��ȥ�ۼ�����ȥ��ʱ��ɴX����
��2������һ������![]() ����λ��ȥ�ۼ���
����λ��ȥ�ۼ���![]() ���������
���������![]() ����λ��ȥ�ۼ���Ҫʹ������
����λ��ȥ�ۼ���Ҫʹ������![]() �����ܹ�������Чȥ�ۣ�����
�����ܹ�������Чȥ�ۣ�����![]() ����Сֵ����ȷ��
����Сֵ����ȷ��![]() ���ο�����:
���ο�����:![]() ȡ
ȡ![]() ��.
��.
���𰸡���1��![]() ��2��
��2��![]()
��������
�����������1����������ȥ�ۼ���Ũ�Ȳ�����![]() ������/��������ʱ����������ȥ�����������Խⲻ��ʽ
������/��������ʱ����������ȥ�����������Խⲻ��ʽ![]() ���ֶ����ã���
���ֶ����ã���![]() ʱ, ��
ʱ, ��![]() ,���
,���![]() .��
.��![]() ʱ, ��
ʱ, ��![]() ,���
,���![]() .����
.���� ![]() ,��2����һ������
,��2����һ������![]() ����λ��ȥ�ۼ���
����λ��ȥ�ۼ���![]() ���Ũ��Ϊ
���Ũ��Ϊ![]() ��������
��������![]() ����λ��ȥ�ۼ���������
����λ��ȥ�ۼ���������![]() ����Ũ��Ϊ
����Ũ��Ϊ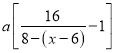 ����˽�����
����˽�����![]() ������Ũ��Ϊ
������Ũ��Ϊ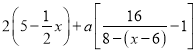 ������
������![]() ��������Ҫ����Ũ����Сֵ��С��4���ɸ��ݻ�������ʽ����Ũ����СֵΪ
��������Ҫ����Ũ����Сֵ��С��4���ɸ��ݻ�������ʽ����Ũ����СֵΪ![]() ���ⲻ��ʽ
���ⲻ��ʽ![]() �����ɵ�
�����ɵ�![]() ����СֵΪ
����СֵΪ![]() .
.
�����������1����Ϊһ������![]() ����λ��ȥ�ۼ�, ���Կ������ͷŵ�Ũ��Ϊ
����λ��ȥ�ۼ�, ���Կ������ͷŵ�Ũ��Ϊ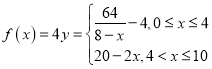 ,
,
��![]() ʱ, ��
ʱ, ��![]() ,���
,���![]() ,����
,����![]() .
.
��![]() ʱ, ��
ʱ, ��![]() ,���
,���![]() ,����
,����![]() .���ǵ�
.���ǵ�![]() ,��һ��Ͷ��
,��һ��Ͷ��![]() ����λ��ȥ�ۼ�, ��Чȥ��ʱ��ɴ�
����λ��ȥ�ۼ�, ��Чȥ��ʱ��ɴ�![]() ��.
��.
��2����ӵ�һ��������, ��![]() ��, Ũ��
��, Ũ��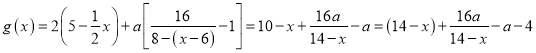 ,
,
��Ϊ![]() ,��
,��![]() ,�ʵ��ҽ���
,�ʵ��ҽ���![]() ʱ,
ʱ,![]() ����СֵΪ
����СֵΪ![]() .
.
��![]() ,���
,���![]() ����СֵΪ
����СֵΪ![]() .
.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ���۲��±���
x | ��3 | ��2 | ��1 | 1 | 2 | 3 |
f��x�� | 5 | 1 | ��1 | ��3 | 3 | 5 |
g��x�� | 1 | 4 | 2 | 3 | ��2 | ��4 |
��f[g��3����f����1��]�� �� ��
A.3
B.4
C.��3
D.5
