题目内容
在数列{an}中,a1=1,an+1=2an+n,记bn=an+n+1,n∈N*.
(Ⅰ)证明:数列{bn}是等比数列;
(Ⅱ)记 ,数列{cn}的前n项和为Sn,求证:
,数列{cn}的前n项和为Sn,求证: .
.
证明:(Ⅰ)由题设an+1=2an+n,得an+1+n+2=2(an+n+1),
即bn+1=2bn. …4分
又b1=a1+1+1=3,所以数列{bn}是其首项为3,且公比为2等比数列.…6分
(Ⅱ)由(I)知,bn=3•2n-1.
于是 . …8分
. …8分
所以cn< . …11分
. …11分
所以Sn=c1+c2+…+cn =
=
 .…14分.
.…14分.
分析:(I)要证明数列{bn}是等比数列,只要证明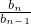 =q≠0即可.利用已知递推关系可转化为证an+1+n+2=2(an+n+1)即得;
=q≠0即可.利用已知递推关系可转化为证an+1+n+2=2(an+n+1)即得;
(II)由(I)知,bn=3•2n-1.于是 从而得出cn<
从而得出cn< .利用此式对和式Sn=c1+c2+…+cn进行放缩后求和即得.
.利用此式对和式Sn=c1+c2+…+cn进行放缩后求和即得.
点评:本题主要考查了等比数列的前n项和、利用定义证明数列为等比数列,考查了数列的递推公式的应用.
即bn+1=2bn. …4分
又b1=a1+1+1=3,所以数列{bn}是其首项为3,且公比为2等比数列.…6分
(Ⅱ)由(I)知,bn=3•2n-1.
于是
 . …8分
. …8分所以cn<
 . …11分
. …11分所以Sn=c1+c2+…+cn
 =
=
 .…14分.
.…14分.分析:(I)要证明数列{bn}是等比数列,只要证明
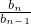 =q≠0即可.利用已知递推关系可转化为证an+1+n+2=2(an+n+1)即得;
=q≠0即可.利用已知递推关系可转化为证an+1+n+2=2(an+n+1)即得;(II)由(I)知,bn=3•2n-1.于是
 从而得出cn<
从而得出cn< .利用此式对和式Sn=c1+c2+…+cn进行放缩后求和即得.
.利用此式对和式Sn=c1+c2+…+cn进行放缩后求和即得.点评:本题主要考查了等比数列的前n项和、利用定义证明数列为等比数列,考查了数列的递推公式的应用.

练习册系列答案
相关题目
 ,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn=
,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn= (n∈N*).
(n∈N*). }的前n项和为Tn,证明:
}的前n项和为Tn,证明: .
.