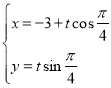题目内容
【题目】过点
的动直线l与y轴交于点
，过点T且垂直于l的直线
与直线
相交于点M.
（1）求M的轨迹方程；
（2）设M位于第一象限，以AM为直径的圆
与y轴相交于点N，且
，求
的值.
【答案】（1）
（2）4
【解析】
（1）动直线l过点
和
，可根据垂直求出直线
，从而求出交点M的坐标，从而寻找横纵坐标的关系，求出点M的轨迹方程. （2）由题意可知：点N即为圆与y轴的切点，根据
，可求出直线AM的斜率，进而求出直线AM的方程，从而求出
的值.
解：（1）∵，，当
时，M的坐标为
当
时，
，∴
，∴的方程为
由
得
，
验证当时，也满足
∴M的坐标满足方程，即M的轨迹方程为
（2）作
轴于
，
轴于
，则
又A为抛物线的焦点，∴
，故圆
与y轴相切于点N
∵，∵
，∴
，∴直线AM的方程为
联立
，消去y整理得
，解得
或
（舍），即
∵A为抛物线的焦点，∴
练习册系列答案
相关题目
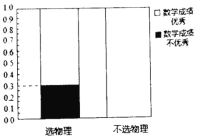
【题目】某省即将实行新高考，不再实行文理分科.某校为了研究数学成绩优秀是否对选择物理有影响，对该校2018级的1000名学生进行调查，收集到相关数据如下：
（1）根据以上提供的信息，完成
列联表，并完善等高条形图；
选物理 | 不选物理 | 总计 | |
数学成绩优秀 | |||
数学成绩不优秀 | 260 | ||
总计 | 600 | 1000 |
（2）能否在犯错误的概率不超过0.05的前提下认为数学成绩优秀与选物理有关？
附：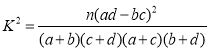
临界值表：
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
