题目内容
（2007•淄博三模）P为△ABC所在平面内一点，且5
-2
-
=
，则△PAB的面积与△ABC的面积的比值为（ ）
| AP |
| AB |
| AC |
| 0 |
分析：根据题意，作出平行四边形ACED，B为AD中点，G、F满足
=
，
=
．根据向量的加法法则，得到
=
+
且
=
+
，根据平行线的性质和三角形面积公式，分别得到△PAB的面积等于平行四边形ACED的
，且△ABC的面积等于平行四边形ACED的
，由此即可得到它们的面积之比．
| AG |
| 2 |
| 5 |
| AB |
| AF |
| 1 |
| 5 |
| AC |
| AE |
| AC |
| AD |
| AP |
| AG |
| AF |
| 1 |
| 20 |
| 1 |
| 4 |
解答：解：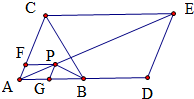
∵5
-2
-
=
∴移项化简，可得
=
+
因此，设向量
=
，
=
，
可得
=
+
点P在以AG、AF为邻边的平行四边形的第四个顶点处，如图所示
平行四边形ACED中，
=
+
B为AD中点，得
=
，
∴△PAB的面积S1=
S△ADE=
S平行四边形ACED
又∵△ABC的面积S2=
S平行四边形ACED
∴S1：S2=
：
=
，即△PAB的面积与△ABC的面积的比值为
故选：D
∵5| AP |
| AB |
| AC |
| 0 |
∴移项化简，可得
| AP |
| 2 |
| 5 |
| AB |
| 1 |
| 5 |
| AC |
因此，设向量
| AG |
| 2 |
| 5 |
| AB |
| AF |
| 1 |
| 5 |
| AC |
可得
| AP |
| AG |
| AF |
点P在以AG、AF为邻边的平行四边形的第四个顶点处，如图所示
平行四边形ACED中，
| AE |
| AC |
| AD |
B为AD中点，得
| AG |
| 1 |
| 5 |
| AD |
∴△PAB的面积S1=
| 1 |
| 10 |
| 1 |
| 20 |
又∵△ABC的面积S2=
| 1 |
| 4 |
∴S1：S2=
| 1 |
| 20 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 5 |
故选：D
点评：本题给出三角形中的向量关系式，求两个三角形的面积之比．着重考查了向量的加法法则、平行四边形的性质和三角形面积公式等知识，属于中档题．
练习册系列答案
相关题目
（2007•淄博三模）正方体ABCD-A1B1C1D1的棱长为1，在正方体表面上与点A距离是