题目内容
8．已知双曲线C：$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1的右顶点为A，渐近线为l1，l2，点P为双曲线C的动点（与点A不重合），过点P作l1的平行线交l2于M，直线AP交l2于N，则|MN|=（ ）| A． | $\frac{3}{2}$ | B． | 2 | C． | $\frac{5}{2}$ | D． | 5 |
分析 求出双曲线的右顶点和渐近线方程，由两直线平行的条件可得l1的平行线，联立方程，求得交点M，N，再由$\sqrt{1+{k}^{2}}$•|x1-x2|，计算即可得到所求值．
解答 解：双曲线C：$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1的右顶点为（4，0），
渐近线方程为l1：y=$\frac{3}{4}$x，l2：y=-$\frac{3}{4}$x，
设P（m，n），即有9m2-16n2=144，
过点P作l1的平行线为y=$\frac{3}{4}$（x-m）+n，
联立直线l2的方程，可得M（$\frac{3m-4n}{6}$，-$\frac{3m-4n}{8}$），
由直线AP的方程y=$\frac{n}{m-4}$（x-4），
联立直线l2的方程，可得N（$\frac{16n}{4n+3m-12}$，-$\frac{12n}{4n+3m-12}$），
即有|MN|=$\sqrt{1+\frac{9}{16}}$•|$\frac{3m-4n}{6}$-$\frac{16n}{4n+3m-12}$|
=$\frac{5}{4}$•|$\frac{9{m}^{2}-16{n}^{2}-36m-48n}{6（4n+3m-12）}$|
=$\frac{5}{4}$•|$\frac{12（12-3m-4n）}{6（4n+3m-12）}$|=$\frac{5}{4}$•2=$\frac{5}{2}$．
故选：C．
点评 本题考查双曲线的方程和性质，主要是渐近线方程的运用，考查两直线的交点的求法，属于中档题．
练习册系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
15．若f（x）=sin（ωx+φ）+cos（ωx+φ）（ω＞0）的最小正周期为π，f（0）=$\sqrt{2}$，则（ ）
| A． | f（x）在$（-\frac{π}{4}，\frac{π}{4}）$单调递增 | B． | f（x）在$（-\frac{π}{4}，\frac{π}{4}）$单调递减 | ||
| C． | f（x）在$（0，\frac{π}{2}）$单调递增 | D． | f（x）在$（0，\frac{π}{2}）$单调递减 |
16．已知sin（α+$\frac{π}{6}$）+cosα=$\frac{4}{5}$$\sqrt{3}$，则cos（2α+$\frac{2π}{3}$）的值为（ ）
| A． | -$\frac{7}{25}$ | B． | $\frac{7}{25}$ | C． | $\frac{9}{25}$ | D． | -$\frac{9}{25}$ |
已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的短轴长为2$\sqrt{3}$，且离心率e=$\frac{1}{2}$，设F1，F2是椭圆的左、右焦点，过F2的直线与椭圆右侧（如图）相交于M，N两点，直线F1M，F1N分别与直线x=4相交于P，Q两点．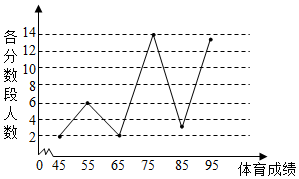
某校高一年级学生全部参加了体育科目的达标测试，现从中随机抽取40名学生的测试成绩，整理数据并按分数段[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]进行分组，假设同一组中的每个数据可用该组区间的中点值代替，则得到体育成绩的折线图（如图）．