题目内容
13.已知函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{5}(1-x)|(x<1)}\\{-(x-2)^{2}+2(x≥1)}\end{array}\right.$,则关于x的方程f(x+$\frac{1}{x}$-2)=a的实根个数不可能为( )| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
分析 以f(x)=1的特殊情形为突破口,解出x=1或3或$\frac{4}{5}$或-4,将x+$\frac{1}{x}$-2是为整体,利用换元的思想方法进一步讨论.
解答 解:∵f(x)=$\left\{\begin{array}{l}{|lo{g}_{5}(1-x)|(x<1)}\\{-(x-2)^{2}+2(x≥1)}\end{array}\right.$,即f(x)=$\left\{\begin{array}{l}{lo{g}_{5}(1-x),x≤0}\\{-lo{g}_{5}(1-x),0<x<1}\\{-(x-2)^{2}+2,x≥1}\end{array}\right.$.
因为当f(x)=1时,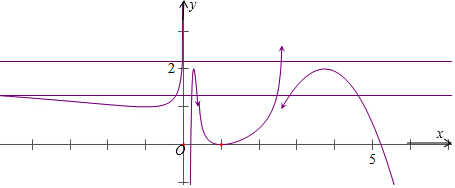
x=1或3或$\frac{4}{5}$或-4,
则当a=1时,
x+$\frac{1}{x}$-2=1或3或$\frac{4}{5}$或-4,
又因为 x+$\frac{1}{x}$-2≥0
或x+$\frac{1}{x}$-2≤-4,
所以,当x+$\frac{1}{x}$-2=-4时只有一个x=-2与之
对应.
其它情况都有2个x值与之对应,
故此时所求的方程有7个根,
当1<a<2时,y=f(x)与y=a有4个交点,
故有8个根;
当a=2时,y=f(x)与y=a有3个交点,
故有6个根;
综上:不可能有5个根,
故选:A.
点评 本题重点考查了分段函数、函数的零点等知识,属于中档题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
5.已知 f(x)=$\frac{lnx}{x}$,其中e 为自然对数的底数,则( )
| A. | f(2)>f(e)>f(3) | B. | f(3)>f(e)>f(2) | C. | f(e)>f(2)>f(3) | D. | f(e)>f(3)>f(2) |
3. 已知正方体ABCD-A1B1C1D1的棱长为1,E为棱CC1的中点,F为棱AA1上的点,且满足A1F:FA=1:2,点F、B、E、G、H为面MBN过三点B、E、F的截面与正方体ABCD-A1B1C1D1在棱上的交点,则下列说法错误的是( )
已知正方体ABCD-A1B1C1D1的棱长为1,E为棱CC1的中点,F为棱AA1上的点,且满足A1F:FA=1:2,点F、B、E、G、H为面MBN过三点B、E、F的截面与正方体ABCD-A1B1C1D1在棱上的交点,则下列说法错误的是( )
 已知正方体ABCD-A1B1C1D1的棱长为1,E为棱CC1的中点,F为棱AA1上的点,且满足A1F:FA=1:2,点F、B、E、G、H为面MBN过三点B、E、F的截面与正方体ABCD-A1B1C1D1在棱上的交点,则下列说法错误的是( )
已知正方体ABCD-A1B1C1D1的棱长为1,E为棱CC1的中点,F为棱AA1上的点,且满足A1F:FA=1:2,点F、B、E、G、H为面MBN过三点B、E、F的截面与正方体ABCD-A1B1C1D1在棱上的交点,则下列说法错误的是( )| A. | HF∥BE | B. | $BM=\frac{{\sqrt{13}}}{2}$ | ||
| C. | ∠MBN的余弦值为$\frac{{\sqrt{65}}}{65}$ | D. | △MBN的面积是$\frac{{\sqrt{61}}}{4}$ |
 如图所示,在三棱柱ABC-A1B1C1中,BB1⊥平面A1B1C1,AC=CB=CC1=2,∠ACB=90°,D、E分别是A1B1、CC1的中点.
如图所示,在三棱柱ABC-A1B1C1中,BB1⊥平面A1B1C1,AC=CB=CC1=2,∠ACB=90°,D、E分别是A1B1、CC1的中点.