题目内容
求sin(2arcsin| 4 | 5 |
分析：根据题意，设arcsin
=α，可得α的范围，由反三角函数的定义，可得sinα=
，根据同角三角函数的基本关系，可得cosα=
；而sin（2arcsin
）=sin2α，由二倍角公式，计算可得答案．
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
解答：解：设arcsin
=α，（0°＜α＜90°），
则sinα=
，根据同角三角函数的基本关系，可得cosα=
；
则sin（2arcsin
）=sin2α=2sinαcosα=
．
| 4 |
| 5 |
则sinα=
| 4 |
| 5 |
| 3 |
| 5 |
则sin（2arcsin
| 4 |
| 5 |
| 24 |
| 25 |
点评：本题考查反三角函数的运用，这类题目的易错点是反三角函数的范围，应特别注意．
练习册系列答案
口算能手系列答案
相关题目
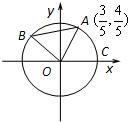如图，A、B是单位圆O上的点，C是圆O与x轴正半轴的交点，点A的坐标为
如图，在四边形ABCD中，AD=8，CD=6，AB=13，∠ADC=90°且