题目内容
 在如图所示的向量
在如图所示的向量| a |
| b |
| c |
| d |
| e |
(1)是共线向量的有
(2)是相反向量的为
(3)相等向量的
(4)模相等的向量
分析:建立直角坐标系,写出向量的坐标
(1)通过向量的坐标得到向量的关系,利用向量共线的充要条件找出共线向量
(2)利用相反向量的定义,从(1)找出相反向量.
(3)利用相等向量的定义:相等向量的坐标相同,得到不存在.
(4)利用向量模的坐标公式求出向量的模,找出模相同的向量.
(1)通过向量的坐标得到向量的关系,利用向量共线的充要条件找出共线向量
(2)利用相反向量的定义,从(1)找出相反向量.
(3)利用相等向量的定义:相等向量的坐标相同,得到不存在.
(4)利用向量模的坐标公式求出向量的模,找出模相同的向量.
解答:解:以
的起点为坐标原点,以矩形的长与宽为x,y轴建立坐标系
则
=(1,2)
=(1,1)
=(1,-2),
=(-1,-2)
=(-2,-2)
(1)∵
=(1,2)
=(-1,-2);
=(1,1),
=(-2,-2)
∴
=-
;
=-2
∴
∥
,
∥
(2)
=-
;
∴
,
是相反向量
(3)无相等向量
(4)∵|
|=
,|
|=
,|
|=
故模相等的向量有
,
,
| a |
则
| a |
| b |
| c |
| d |
| e |
(1)∵
| a |
| d |
| b |
| e |
∴
| a |
| d |
| e |
| b |
∴
| a |
| d |
| e |
| b |
(2)
| a |
| d |
∴
| a |
| d |
(3)无相等向量
(4)∵|
| a |
| 5 |
| c |
| 5 |
| d |
| 5 |
故模相等的向量有
| a |
| c |
| d |
点评:本题考查通过建立直角坐标系将向量问题转化为坐标形式的向量问题、共线向量、相等向量、相反向量的定义.

练习册系列答案
相关题目
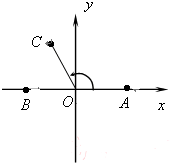 在如图所示的平面直角坐标系中,已知点.A(1,0)和点B(-1,0),
在如图所示的平面直角坐标系中,已知点.A(1,0)和点B(-1,0), 在如图所示的平面直角坐标系中,已知点.A(1,0)和点B(-1,0),
在如图所示的平面直角坐标系中,已知点.A(1,0)和点B(-1,0), ,且∠AOC=x,其中O为坐标原点.
,且∠AOC=x,其中O为坐标原点. ,设点D为线段OA上的动点,求
,设点D为线段OA上的动点,求 的最小值;
的最小值; ,向量
,向量 ,
, ,求
,求 的最小值及对应的x值.
的最小值及对应的x值. ,且∠AOC=x,其中O为坐标原点.
,且∠AOC=x,其中O为坐标原点. ,设点D为线段OA上的动点,求
,设点D为线段OA上的动点,求 的最小值;
的最小值; ,向量
,向量 ,
, ,求
,求 的最小值及对应的x值.
的最小值及对应的x值.
 ,且∠AOC=x,其中O为坐标原点.
,且∠AOC=x,其中O为坐标原点. ,设点D为线段OA上的动点,求
,设点D为线段OA上的动点,求 的最小值;
的最小值; ,向量
,向量 ,
, ,求
,求 的最小值及对应的x值.
的最小值及对应的x值.