题目内容
在如图所示的平面直角坐标系中,已知点.A(1,0)和点B(-1,0), ,且∠AOC=x,其中O为坐标原点.
,且∠AOC=x,其中O为坐标原点.(Ⅰ)若
 ,设点D为线段OA上的动点,求
,设点D为线段OA上的动点,求 的最小值;
的最小值;(Ⅱ)若
 ,向量
,向量 ,
, ,求
,求 的最小值及对应的x值.
的最小值及对应的x值.
【答案】分析:(Ⅰ) 设D(t,0)(0≤t≤1),化简  =
= ,利用二次函数的性质求得它的最小值.
,利用二次函数的性质求得它的最小值.
(Ⅱ)由题意得 =1-
=1- sin(2x+
sin(2x+ ),再利用
),再利用
正弦函数的定义域和值域 求出它的最小值.
解答:解:(Ⅰ)若 ,设D(t,0)(0≤t≤1),可得
,设D(t,0)(0≤t≤1),可得 ,
,
所以, ,
,
所以 …(3分)
…(3分)
= ,
,
所以当 时,
时, 取得最小值为
取得最小值为 ,故
,故 最小值为
最小值为 .…(6分)
.…(6分)
(Ⅱ)由题意得C(cosx,sinx),
则 =1-
=1- sin(2x+
sin(2x+ ).…(9分)
).…(9分)
因为 ,所以
,所以 .
.
所以当 ,即
,即 时,
时, 取得最大值1,
取得最大值1,
所以 时,
时, 取得最小值
取得最小值 ,
,
所以 的最小值为
的最小值为 ,此时
,此时 . …(12分)
. …(12分)
点评:本题主要考查三角函数的恒等变换及化简求值,两个向量的数量积的公式,正弦函数的定义域和值域,属于中档题.
 =
= ,利用二次函数的性质求得它的最小值.
,利用二次函数的性质求得它的最小值.(Ⅱ)由题意得
 =1-
=1- sin(2x+
sin(2x+ ),再利用
),再利用正弦函数的定义域和值域 求出它的最小值.
解答:解:(Ⅰ)若
 ,设D(t,0)(0≤t≤1),可得
,设D(t,0)(0≤t≤1),可得 ,
,所以,
 ,
,所以
 …(3分)
…(3分)=
 ,
,所以当
 时,
时, 取得最小值为
取得最小值为 ,故
,故 最小值为
最小值为 .…(6分)
.…(6分)(Ⅱ)由题意得C(cosx,sinx),

则
 =1-
=1- sin(2x+
sin(2x+ ).…(9分)
).…(9分)因为
 ,所以
,所以 .
.所以当
 ,即
,即 时,
时, 取得最大值1,
取得最大值1,所以
 时,
时, 取得最小值
取得最小值 ,
,所以
 的最小值为
的最小值为 ,此时
,此时 . …(12分)
. …(12分)点评:本题主要考查三角函数的恒等变换及化简求值,两个向量的数量积的公式,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 已知函数f(x)=x2-2|x|-1.
已知函数f(x)=x2-2|x|-1.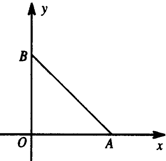 在如图所示的平面直角坐标系中,三角形AOB是腰长为2的等腰直角三角形,动点P与点O位于直线AB的两侧,且∠APB=
在如图所示的平面直角坐标系中,三角形AOB是腰长为2的等腰直角三角形,动点P与点O位于直线AB的两侧,且∠APB= 已知函数f(x)=x2-2|x|-1.
已知函数f(x)=x2-2|x|-1. (2012•盐城一模)在综合实践活动中,因制作一个工艺品的需要,某小组设计了如图所示的一个门(该图为轴对称图形),其中矩形ABCD的三边AB、BC、CD由长6分米的材料弯折而成,BC边的长为2t分米(
(2012•盐城一模)在综合实践活动中,因制作一个工艺品的需要,某小组设计了如图所示的一个门(该图为轴对称图形),其中矩形ABCD的三边AB、BC、CD由长6分米的材料弯折而成,BC边的长为2t分米(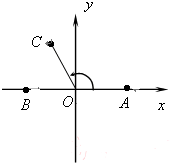 在如图所示的平面直角坐标系中,已知点.A(1,0)和点B(-1,0),
在如图所示的平面直角坐标系中,已知点.A(1,0)和点B(-1,0),