题目内容
数列{an}满足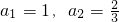 ,且
,且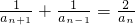 (n≥2),则an=________.
(n≥2),则an=________.
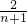
分析:根据
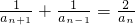 (n≥2),判断出数列
(n≥2),判断出数列 是以
是以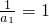 为首项,以
为首项,以 为公差的等差数列,利用等差数列的通项公式求出
为公差的等差数列,利用等差数列的通项公式求出 =
= ,进一步求出an=
,进一步求出an=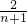 .
.解答:因为数列{an}满足
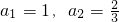 ,且
,且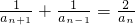 (n≥2),
(n≥2),所以数列
 是以
是以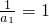 为首项,以
为首项,以 为公差的等差数列,
为公差的等差数列,所以
 =
= ,
,所以an=
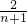 .
.故答案为
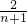 .
.点评:本题考查通过构造新数列来求数列的通项公式,再求数列的通项公式时,应该根据所给通项公式的特点选择合适的求通项方法.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
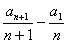 =1,且
=1,且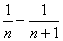 =2(n∈N*),则a10为( )
=2(n∈N*),则a10为( )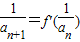 ,且a1=4,求数列an的通项公式;
,且a1=4,求数列an的通项公式;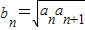 ,数列bn的前n项和Tn,求证:
,数列bn的前n项和Tn,求证: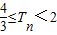 .
.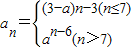 且{an}是递增数列,则实数a的范围是( )
且{an}是递增数列,则实数a的范围是( )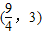
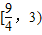
 ,且a1=4,求数列{an} 的通项公式;
,且a1=4,求数列{an} 的通项公式;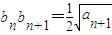 ,当n≥3,n∈N*时,求证:①
,当n≥3,n∈N*时,求证:①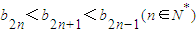 ;②
;②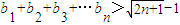 .
.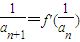 ,且a1=4,求数列an的通项公式;
,且a1=4,求数列an的通项公式; ,数列bn的前n项和Tn,求证:
,数列bn的前n项和Tn,求证: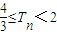 .
.