题目内容
若椭圆 +
+ =1的焦点在x轴上,过点(1,
=1的焦点在x轴上,过点(1, )作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是________.
)作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是________.

分析:设过点(1,
 )的圆x2+y2=1的切线为l,根据直线的点斜式,结合讨论可得直线l分别切圆x2+y2=1相切于点A(1,0)和B(0,2).然后求出直线AB的方程,从而得到直线AB与x轴、y轴交点坐标,得到椭圆的右焦点和上顶点,最后根据椭圆的基本概念即可求出椭圆的方程.
)的圆x2+y2=1的切线为l,根据直线的点斜式,结合讨论可得直线l分别切圆x2+y2=1相切于点A(1,0)和B(0,2).然后求出直线AB的方程,从而得到直线AB与x轴、y轴交点坐标,得到椭圆的右焦点和上顶点,最后根据椭圆的基本概念即可求出椭圆的方程.解答:设过点(1,
 )的圆x2+y2=1的切线为l:y-
)的圆x2+y2=1的切线为l:y- =k(x-1),即kx-y-k+
=k(x-1),即kx-y-k+ =0
=0①当直线l与x轴垂直时,k不存在,直线方程为x=1,恰好与圆x2+y2=1相切于点A(1,0);
②当直线l与x轴不垂直时,原点到直线l的距离为:d=
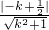 =1,解之得k=-
=1,解之得k=- ,
,此时直线l的方程为y=-
 x+
x+ ,l切圆x2+y2=1相切于点B(
,l切圆x2+y2=1相切于点B(  ,
, );
);因此,直线AB斜率为k1=
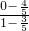 =-2,直线AB方程为y=-2(x-1)
=-2,直线AB方程为y=-2(x-1)∴直线AB交x轴交于点A(1,0),交y轴于点C(0,2).
椭圆
 +
+ =1的右焦点为(0,1),上顶点为(0,2)
=1的右焦点为(0,1),上顶点为(0,2)∴c=1,b=2,可得a2=b2+c2=5,椭圆方程为

故答案为:
 .
.点评:本题考查椭圆的简单性质、圆的切线的性质、椭圆中三参数的关系:a2=b2+c2.

练习册系列答案
相关题目
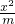 +
+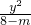 =1.
=1.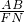 是定值,并求出这个定值.
是定值,并求出这个定值.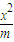 +
+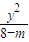 =1.
=1.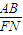 是定值,并求出这个定值.
是定值,并求出这个定值.